参考资料:A Mathematical Theory of Communication
信号和噪声
- 信号
- 电声学
- 根据换能器和数字信号处理,我们可以将声能转换为电能,得到基带信号
- 微电子
- 电磁学
- 根据天线理论的电磁波,我们可以使用射频的电磁波,向空间发射信号
- 电声学
- 信号在空间中传播,经过的道路称为信道,信道中可能含有大量噪声源
- 由Fourier变换和中心极限定理可知,对于大量独立、同分布的噪声源
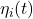 ,在任意时刻
,在任意时刻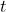 ,
,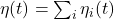 接近于Gauss变量
接近于Gauss变量 - 如果信道具有独立、加性的噪声,那么
![Rendered by QuickLaTeX.com \[ Y(t) = X(t) + \eta(t), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4a104091fbe6e0ab8cb7ee5367793255_l3.png)
进一步,如果噪声的均值为0,那么信号和噪声混合后的平均功率![Rendered by QuickLaTeX.com \[ \mathbb{E}[Y(t)^2] = \mathbb{E}[X(t)^2] + 2\mathbb{E}[X(t)] \cdot \mathbb{E}[\eta(t)] + \mathbb{E}[\eta(t)^2]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-277dd7aa5149aa9fb45517647df44524_l3.png)
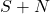 ,等于信号的平均功率
,等于信号的平均功率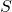 ,加上噪声的平均功率
,加上噪声的平均功率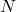
- 因此,我们考虑噪声和随机过程中的加性Gauss白噪声,
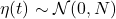
- 由Fourier变换和中心极限定理可知,对于大量独立、同分布的噪声源
Shannon熵、微分熵
- 在Shannon熵中,我们可以得到,Shannon熵给出了最小平均长度的最佳估计——无论信息如何压缩,其长度下界为Shannon熵。因此,Shannon熵可以视为信息量
- 离散情形 –> Shannon熵
![Rendered by QuickLaTeX.com \[ H(X) = -\sum_{i = 1}^n \mathbb{P}(x_i)\log_2\mathbb{P}(x_i), \text{ where } \sum_{i = 1}^n \mathbb{P}(x_i) = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-468f904dfb6850e49b21f08f4601fa9b_l3.png)
- 连续情形 –> 微分熵
![Rendered by QuickLaTeX.com \[ h(X) = -\int_{-\infty}^{+\infty} p_X(x)\ln p_X(x)dx, \text{ where } \int_{-\infty}^{+\infty} p_X(x)dx = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6723c3992b455e2a87602b1aa89d3e80_l3.png)
- Gauss变量的微分熵
注意,当![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} h(X) &= \int_{-\infty}^{+\infty} p_X(x)\bigg[\frac 12\ln(2\pi\sigma^2) + \frac{(x - \mu)^2}{2\sigma^2}\bigg]dx \\ &= \frac 12\ln(2\pi\sigma^2) + \frac{1}{2\sigma^2} \cdot \sigma^2 \\ &= \frac 12\ln(2\pi e\sigma^2). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6bfac5738ef2afeea5c92bf96f0e6c26_l3.png)
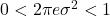 时,我们有
时,我们有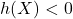 。微分熵可以为负,而Shannon熵一定为非负,所以二者具有本质的不同
。微分熵可以为负,而Shannon熵一定为非负,所以二者具有本质的不同
- 离散情形 –> Shannon熵
- 数字信号、模拟信号
- 数字信号为离散情形,通常以
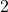 为底数,单位为bit(比特)
为底数,单位为bit(比特) - 模拟信号为连续情形,通常以自然常数
 为底数,单位为nat(奈特)
为底数,单位为nat(奈特) - 由对数的换底公式可知,Shannon熵、微分熵取不同底数只相差常数倍。在下面的计算中,为了方便起见,我们以
 为底数
为底数
- 数字信号为离散情形,通常以
- 信息传输率为
进一步,信道容量为信息传输率的理论极限,![Rendered by QuickLaTeX.com \[ R = h(Y) - h(Y|X). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6e5f6b59716f70bc86e884b97311822b_l3.png)
![Rendered by QuickLaTeX.com \[ C = \sup_{p_X} R. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e36103a27039ff0e94f6b1749c9134e9_l3.png)
- 信源发送的信号为
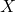 ,目的端接收的信号为
,目的端接收的信号为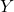 。因此,信息传输率可以视为目的端接收到的信息量
。因此,信息传输率可以视为目的端接收到的信息量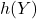 ,减去损耗的信息量
,减去损耗的信息量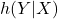
- 在Shannon熵中,我们固定信源、遍历编码,得到最小平均长度,所以它反映了信源的特征。在这里,我们固定信道、遍历信源,得到信道容量,所以它反映了信道的特征
- 信源发送的信号为
- 计算
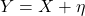 的信道容量
的信道容量
- 条件概率密度函数
因此,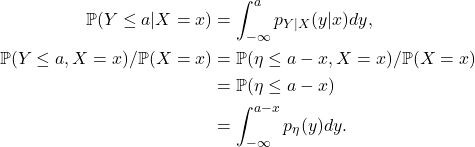
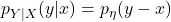
- 条件熵
![Rendered by QuickLaTeX.com \[ h(Y|X = x) = -\int_{-\infty}^{+\infty} p_\eta(y - x)\ln p_\eta(y - x)dy = h(\eta), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-15ed9910935dfefc2d426245edbfaa36_l3.png)
![Rendered by QuickLaTeX.com \[ h(Y|X) = \int_{-\infty}^{+\infty} p_X(x)h(\eta)dx = h(\eta). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c84df22965bca136aa7fc70c4e3867f2_l3.png)
- 信息传输率、信道容量
因此,我们需要最大化微分熵,这是一个最优化问题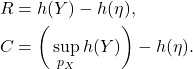
- 条件概率密度函数
求解最优化问题
- 求解最优化问题的第一种方法是Lagrange乘子法。对于离散情形,我们需要多元函数和偏导数;对于连续情形,我们需要泛函和变分
- (离散情形 –> Shannon熵)目标函数为
约束条件为![Rendered by QuickLaTeX.com \[ H(p_1, \ldots, p_n) = -\sum_{i = 1}^n p_i\ln p_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2ae4b8ab00cdd3ac3339b4e0b0e5e49b_l3.png)
![Rendered by QuickLaTeX.com \[ \varphi_1 = \sum_{i = 1}^n p_i - 1 = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-26b1082be5b4893f1dfe231b6cf1ea0d_l3.png)
- 令
那么,![Rendered by QuickLaTeX.com \[ L = H(p_1, \ldots, p_n) + a\varphi_1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-49a652a9c34415abe78f1897eb3ae2b7_l3.png)
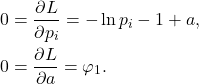
- 由第一个方程,所有
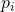 都相等。由第二个方程,
都相等。由第二个方程,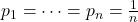
- 令
- (连续情形 –> 微分熵)目标泛函为
约束条件为![Rendered by QuickLaTeX.com \[ h(p) = -\int_{-\infty}^{+\infty} p(x)\ln p(x)dx. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3d01936cf5028bc6be12a02a615d3e01_l3.png)

- 令
那么,![Rendered by QuickLaTeX.com \[ L = h(p) + a\varphi_1 + b\varphi_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-556847738cd945a4cf8cdadcd12d5131_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} 0 &= \delta L = \int_{-\infty}^{+\infty} [-\ln p(x) - 1 + a + bx^2]\delta pdx, \\ 0 &= \frac{\partial L}{\partial a} = \varphi_1,\; 0 = \frac{\partial L}{\partial b} = \varphi_2. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f8867614c30867f1681a3a4d09f23a61_l3.png)
- 由第一个方程,
由其余的方程,![Rendered by QuickLaTeX.com \[ -\ln p(x) -1 + a + bx^2 = 0,\; p(x) = e^{-1 + a + bx^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8a40caa6d40a1b36daa2ccc84843121b_l3.png)
![Rendered by QuickLaTeX.com \[ p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9764983bc40b0aa4fbf623ee7cbd2199_l3.png)
- 之所以增加二阶矩的约束条件,是因为平均功率是已知的。如果不增加约束条件,那么
 为不可积的常数;如果增加一阶矩的约束条件,那么
为不可积的常数;如果增加一阶矩的约束条件,那么 为指数函数,它至多在实数轴的一个方向上可积
为指数函数,它至多在实数轴的一个方向上可积
- 令
- (离散情形 –> Shannon熵)目标函数为
- 求解最优化问题的第二种方法是使用KL散度,它通常用于深度学习,比如降噪扩散概率模型(Denoising Diffusion Probabilistic Model,DDPM)
- KL散度、交叉熵(Cross Entropy,CE)
因此,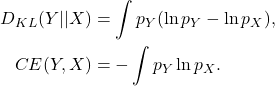
![Rendered by QuickLaTeX.com \[ D_{KL}(Y || X) = -h(Y) + CE(Y, X). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6807f7e74c271a0b23ae682464e4e4d4_l3.png)
- 由Jensen不等式,KL散度非负,
等式成立当且仅当![Rendered by QuickLaTeX.com \[ D_{KL}(Y || X) = -\int p_Y\ln\bigg(\frac{p_X}{p_Y}\bigg) \geq -\ln\bigg(\int p_Y\frac{p_X}{p_Y}\bigg) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-145cb59681beffe6541c8151b8d264c7_l3.png)
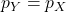 。因此,KL散度可以用于衡量两个概率分布之间的接近程度。在Shannon熵中,证明最小平均长度的下界为Shannon熵,恰好使用了KL散度非负
。因此,KL散度可以用于衡量两个概率分布之间的接近程度。在Shannon熵中,证明最小平均长度的下界为Shannon熵,恰好使用了KL散度非负 - 对于约束条件
![Rendered by QuickLaTeX.com \mathbb{E}[Y^2] = \sigma^2](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bfe4ef58fc81b3bef2e2a2354b9e62af_l3.png) ,取
,取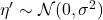 。利用KL散度非负,
。利用KL散度非负,
同时,交叉熵为![Rendered by QuickLaTeX.com \[ h(Y) \leq CE(Y, \eta'). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-77f304d51401c19f08db696b3a439dc4_l3.png)
因此,当![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} CE(Y, \eta') &= \int p_Y\bigg[\frac 12\ln(2\pi\sigma^2) + \frac 12\frac{x^2}{\sigma^2}\bigg] \\ &= \frac 12\ln(2\pi\sigma^2) + \frac{1}{2\sigma^2}\mathbb{E}[Y^2] \\ &= \frac 12\ln(2\pi e\sigma^2). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-17d3ecf13a89c13c74f35163c20fc987_l3.png)
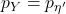 时,即
时,即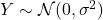 时,
时,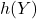 达到最大值
达到最大值
- KL散度、交叉熵(Cross Entropy,CE)
Shannon公式和信噪比
- 现在,我们回到信号和噪声中的讨论。
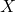 的平均功率为
的平均功率为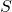 ,
,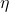 的平均功率为
的平均功率为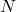 ,
,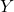 的平均功率为
的平均功率为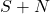
- 由噪声和随机过程可知,当
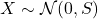 ,
,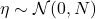 时,我们有
时,我们有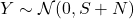 。此时,
。此时,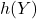 达到最大值,信道容量为
达到最大值,信道容量为![Rendered by QuickLaTeX.com \[ C = \frac 12\ln[2\pi e(S + N)] - \frac 12\ln(2\pi eN) = \frac 12\ln\bigg(1 + \frac SN\bigg). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e1ce2a5c0e32a239a0283782741e482b_l3.png)
- 只有发送Gauss噪声时,信息传输率才能达到信道容量。如果发送有意义的信号,那么信息传输率小于信道容量
- 大量独立、同分布的噪声混合,得到Gauss噪声;Gauss噪声和Gauss噪声混合,仍然得到Gauss噪声。因此,Gauss噪声是一种在混合下最均匀的噪声
- 由噪声和随机过程可知,当
- 设模拟信道的带宽为
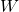
- 根据换能器和数字信号处理,从模拟信号到数字信号需要进行采样
- 根据频率响应和采样率,我们用Nyquist采样率
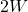 来采样
来采样 - 最终,我们可以得到数字信道的Shannon公式(我们将底数重新变为
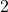 )
)![Rendered by QuickLaTeX.com \[ C = 2W \times \frac 12\log_2\bigg(1 + \frac SN\bigg) = W\log_2\bigg(1 + \frac SN\bigg)\; (bit/s). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a3c83d58fd7b8cb17f938df15cc096a9_l3.png)
- 模拟信道的带宽是指
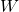 ,单位为Hz;数字信道的带宽是指
,单位为Hz;数字信道的带宽是指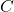 ,单位为bit/s。数字信道基于模拟信道,它的带宽既取决于模拟信道的带宽
,单位为bit/s。数字信道基于模拟信道,它的带宽既取决于模拟信道的带宽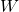 ,也取决于信噪比
,也取决于信噪比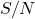
- 采样是在时间上的离散化,量化是在空间上的离散化。量化会产生量化噪声,我们可以计算量化信噪比
- 设信号的取值范围为
![Rendered by QuickLaTeX.com [-A, A]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-69f8fd7ff048e74b3bec8f8dd87aee1d_l3.png) 。如果信号均匀分布,那么信号的平均功率为
。如果信号均匀分布,那么信号的平均功率为![Rendered by QuickLaTeX.com \[ S = \int_{-A}^A x^2 \cdot \frac{1}{2A}dx = \frac 13A^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ca52862a78d779c5221813778a08948c_l3.png)
- 现在,我们用
 位二进制数来表示信号
位二进制数来表示信号
- 将区间分为
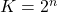 段,每段的长度为
段,每段的长度为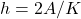 ,
,![Rendered by QuickLaTeX.com \[ [-A + ih, -A + (i + 1)h],\; 0 \leq i \leq K - 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-591b3bda1cf53dfb14bce8b6e9e401f4_l3.png)
- 将
 位二进制数映射到每段的中心点
位二进制数映射到每段的中心点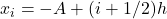 ,每段的值判决为中心点,量化噪声的平均功率为
,每段的值判决为中心点,量化噪声的平均功率为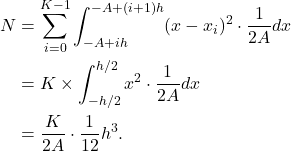
- 将区间分为
- 最终,量化信噪比为
![Rendered by QuickLaTeX.com \[ \frac SN = \frac 8K \cdot \frac{A^3}{h^3} = \frac 8K \cdot \frac{K^3}{8} = 2^{2n}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-93e0611bed4a7b94f084dc1118e6bdff_l3.png)
- 设信号的取值范围为
- 因为量化信噪比的动态范围大,所以我们以
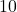 为底数取对数,单位为B(贝)
为底数取对数,单位为B(贝)
在实际应用中,我们再乘以10,单位为dB(分贝)![Rendered by QuickLaTeX.com \[ \log_{10} \frac SN = 2n\log_{10}2 \approx 0.6n\; (B). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d7077f517776321f21e7f719a3def994_l3.png)
![Rendered by QuickLaTeX.com \[ 10\log_{10} \frac SN \approx 6n\; (dB). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fa8ca5f10099da7e7a2fbe95533701cb_l3.png)
- 对于二进制数,我们通常认为0、1出现的概率相等(即1/2),1位二进制数的Shannon熵恰好为1bit。因此,量化使用的二进制位数
 称为位深,单位为bit
称为位深,单位为bit
- 对于CD格式,位深为16bit,量化信噪比约为96dB
- 对于老式的电子游戏音乐,位深为8bit,量化信噪比约为48dB