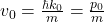电磁波
- 关于电磁波,可参见Maxwell方程组。关于时频分析,可参见频率响应和采样率
- 电磁波满足波动方程
按照时频分析的观点,我们尝试分离出角频率![Rendered by QuickLaTeX.com \[ \frac{1}{c^2}\partial_{tt}\psi = \Delta\psi. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d4351d88173d527684c7b3a851d5b2af_l3.png)
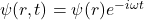 ,然后求解齐次Helmholtz方程
,然后求解齐次Helmholtz方程![Rendered by QuickLaTeX.com \[ \Delta\psi + \frac{\omega^2}{c^2}\psi = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4b4767cda54a2088096fb1ed941dba60_l3.png)
- 不同于时频分析,我们使用如下形式的Fourier变换、Fourier逆变换
因此,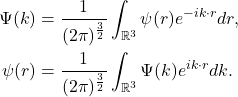
![Rendered by QuickLaTeX.com \[ \bigg(-|k|^2 + \frac{\omega^2}{c^2}\bigg)\Psi = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-726b42e340043ac94129931ccfbf1bbc_l3.png)
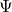 几乎为0,不过不包括
几乎为0,不过不包括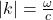 的点,所以我们尝试取一个解
的点,所以我们尝试取一个解![Rendered by QuickLaTeX.com \[ \Psi(k) = \delta(k - k_0),\; |k_0| = \frac{\omega}{c}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2eaa54bd76154ecd8c7358d410468b57_l3.png)
这对应于平面波的解,原因是对于任意时刻![Rendered by QuickLaTeX.com \[ \psi(r, t) = \frac{1}{(2\pi)^{\frac 32}}e^{ik_0 \cdot r}e^{-i\omega t} = \frac{1}{(2\pi)^{\frac 32}}e^{i(k_0 \cdot r - \omega t)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b55d69a530154c71dba2080ca6ebce42_l3.png)
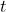 ,波前为等势面
,波前为等势面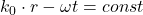 ,这是一个平面。随着
,这是一个平面。随着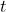 增加,
增加,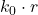 也增加,所以传播方向为
也增加,所以传播方向为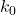
- 将平面波线性叠加,可得
其中,色散关系为![Rendered by QuickLaTeX.com \[ \psi(r, t) = \frac{1}{(2\pi)^{\frac 32}}\int_{\mathbb{R}^3} \Psi(k)e^{i(k \cdot r - \omega t)}dk, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-135308f2502c5658b00bb5b83bccde5e_l3.png)
![Rendered by QuickLaTeX.com \[ \omega(k) = c|k|. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e6ca0053c9bcc7caa08ec8d2dfb87ca_l3.png)
导出Schrödinger方程
- 为了得到量子化的物质波,我们使用Einstein光电效应方程
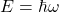 ,以及de Broglie物质波方程
,以及de Broglie物质波方程 ,从而
,从而
因此,色散关系为![Rendered by QuickLaTeX.com \[ \hbar\omega = E = \frac{|p|^2}{2m} = \frac{\hbar^2|k|^2}{2m}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d7000fe0ee246e6f6f317704c96b13eb_l3.png)
![Rendered by QuickLaTeX.com \[ \omega(k) = \frac{\hbar|k|^2}{2m}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9cd75045cdb5817be6edb68a321d7c14_l3.png)
- 由此可得,
故波函数![Rendered by QuickLaTeX.com \[ \psi(r, t) = \frac{1}{(2\pi)^{\frac 32}}\int_{\mathbb{R}^3} \Psi(k)e^{i(k \cdot r - \frac{\hbar|k|^2}{2m}t)}dk. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-50c65c4a19c2d430ee7843b4f7df30e8_l3.png)
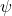 满足Schrödinger方程
满足Schrödinger方程![Rendered by QuickLaTeX.com \[ \partial_t\psi = \frac{-i\hbar|k|^2}{2m}\frac{1}{(2\pi)^{\frac 32}}\int_{\mathbb{R}^3} \Psi(k)e^{i(k \cdot r - \frac{\hbar |k|^2}{2m}t)}dk = \frac{i\hbar}{2m}\Delta\psi. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-110e5e74e29903cf27372bf4ce76a201_l3.png)
- 波动方程的色散关系为1次的,而Schrödinger方程的色散关系为2次的,所以前者需要时间的2阶导数,而后者只需要时间的1阶导数。在使用Fourier变换求解PDE中,Schrödinger方程和热方程具有相同的解法,并且形式上更加接近这里使用的Fourier变换
波函数和粒子
- 当
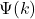 只在
只在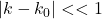 范围内非零时,我们认为波函数
范围内非零时,我们认为波函数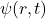 接近于粒子
接近于粒子 - 计算扰动
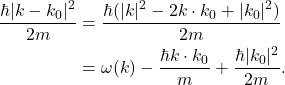
- 如果我们忽略
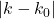 的二阶项,那么
的二阶项,那么
因此,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \psi(r, t) &= \frac{1}{(2\pi)^{\frac 32}}\int_{\mathbb{R}^3} \Psi(k)e^{i[k \cdot r - \omega(k)t]}dk \\ &\approx \frac{1}{(2\pi)^{\frac 32}}\int_{\mathbb{R}^3} \Psi(k)e^{i[k \cdot (r - \frac{\hbar k_0}{m}t) + \frac{\hbar|k_0|^2}{2m}t]}dk \\ &= e^{i\frac{\hbar|k_0|^2}{2m}t}\psi\bigg(r - \frac{\hbar k_0}{m}t, 0\bigg). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-de7b61fbf3e8e318dded13bb59032c5f_l3.png)
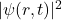 保持不变,粒子的速度为
保持不变,粒子的速度为