正整数
import math
// (n) -> (factor)
def find_factor(n):
factor = 1
// If n = ab, 1 < a <= b < n, then 2 <= a <= floor(sqrt(n))
upper_bound = math.floor(math.sqrt(n))
for i in range(2, upper_bound + 1):
if n % i == 0:
factor = i
break
return factor
// (n) -> (result)
def is_prime(n):
result = False
if find_factor(n) == 1:
result = True
return result
print(is_prime(23))
print(is_prime(233))
print(is_prime(2333))
print(is_prime(23333))
print(is_prime(233333))
print(find_factor(233333))
// ----- Run Program -----
> python arithmetic.py
True
True
True
True
False
353
Euclid算法
// (a, b) -> (q, r)
def division_with_remainder(a, b):
// Python does not behave as the above definition, so we only consider positive integers
q = a // b
r = a % b
return (q, r)
// (a, b) -> (d, m, n)
def Euclidean_algorithm(a, b):
d = 0; m = 0; n = 0
dividend = a; divisor = b
// dividend = mi * a + ni * b
mi = 1; ni = 0
// divisor = oi * a + pi * b
oi = 0; pi = 1
while(divisor != 0):
(qi, ri) = division_with_remainder(dividend, divisor)
dividend = divisor
divisor = ri
(mi, ni, oi, pi) = (oi, pi, mi - qi * oi, ni - qi * pi)
d = dividend
m = mi
n = ni
return (d, m, n)
print(division_with_remainder(2333, 233))
print(division_with_remainder(233, 2333))
a = 233; b = 2333
(d, m, n) = Euclidean_algorithm(a, b)
print(d, m, n)
print(m * a + n * b)
// ----- Run Program -----
> python arithmetic.py
(10, 3)
(0, 233)
1 -781 78
1
素因子分解
// (n) -> (prime_factors)
def prime_factorization(n):
prime_factors = []
recursive_factor(n, prime_factors)
return prime_factors
// (n, prime_factors) -> ()
def recursive_factor(n, prime_factors):
if is_prime(n):
prime_factors.append(n)
else:
a = find_factor(n)
b = n // a
recursive_factor(a, prime_factors)
recursive_factor(b, prime_factors)
print(prime_factorization(233333))
print(prime_factorization(123456789))
// ----- Run Program -----
> python arithmetic.py
[353, 661]
[3, 3, 3607, 3803]
Eratosthenes筛法
// (n) -> (all_primes)
def Eratosthenes_sieve(n):
// Create a list from 2 to n
all_primes = list(range(2, n + 1))
p = 2
while(max(all_primes) > p):
// Remove 2p, 3p, ..., floor(n / p) * p from the list
for i in range(2, math.floor(n / p) + 1):
if i * p in all_primes:
all_primes.remove(i * p)
// Find the smallest number greater than p in the list
for i in range(len(all_primes)):
if all_primes[i] > p:
p = all_primes[i]
break
return all_primes
print(Eratosthenes_sieve(233))
n = 233
print(len(Eratosthenes_sieve(n)) / (n / math.log(n)))
n = 2333
print(len(Eratosthenes_sieve(n)) / (n / math.log(n)))
n = 23333
print(len(Eratosthenes_sieve(n)) / (n / math.log(n)))
// ----- Run Program -----
> python arithmetic.py
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233]
1.1931457559306897
1.146782702034888
1.1215847730217052
Diophantus方程
![Rendered by QuickLaTeX.com \[ \mathbb{Z}_+ = \{ 1, 2, 3, \ldots \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc7fe2d50983fa2bf402aa20b9bc6d5c_l3.png)
 、
、 、
、 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ n = ab, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-822906016ca4b418d3e20b8f09e25e17_l3.png)
 、
、 整除(Divide)
整除(Divide) ,记为
,记为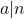 、
、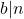
 、
、 称为
称为 的除子(Divisor)或因子(Factor)。在代数几何中,我们通常使用除子;在算术中,我们通常使用因子
的除子(Divisor)或因子(Factor)。在代数几何中,我们通常使用除子;在算术中,我们通常使用因子 称为
称为 、
、 的倍数(Multiple)
的倍数(Multiple) 的因子只有
的因子只有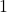 、
、 ,那么
,那么 称为素数(Prime Number)
称为素数(Prime Number)![Rendered by QuickLaTeX.com \[ \mathbb{Z} = \{ 0, \pm 1, \pm 2, \pm 3, \ldots \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d5b81c906b2ce7ec9b2c566c6b3739dc_l3.png)
 、
、 、
、 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ n = ab, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-822906016ca4b418d3e20b8f09e25e17_l3.png)
 、
、 整除
整除 ,记为
,记为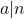 、
、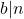
 、
、 称为
称为 的除子或因子
的除子或因子 称为
称为 、
、 的倍数
的倍数 的因子只有
的因子只有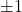 、
、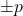 ,那么
,那么 称为素数。注意,
称为素数。注意,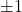 不是素数,而是单位(Unit),所以上面的is_prime()不适用于
不是素数,而是单位(Unit),所以上面的is_prime()不适用于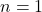
 、
、 为整数,
为整数,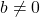
![Rendered by QuickLaTeX.com \[ a, a \pm b, a \pm 2b, a \pm 3b, \ldots \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4f0d72bbaadcc1f9bfde67c53879109e_l3.png)
![Rendered by QuickLaTeX.com \[ r = a + qb,\; q \in \mathbb{Z}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dde9801d23d22d5b6927d151a2fea98b_l3.png)
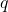 称为商(Quotient)
称为商(Quotient)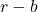 、
、 的符号相反(否则,
的符号相反(否则, 不是最小的非负整数)。因此,
不是最小的非负整数)。因此,![Rendered by QuickLaTeX.com \[ (r - b)(r + b) < 0,\; 0 \leq r < |b|, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-de6de17fa85fdcba356c9ccd3621e616_l3.png)
 称为余数(Remainder)
称为余数(Remainder) 为被除数(Dividend),
为被除数(Dividend), 为除数(Divisor)。如果除数为0,那么一种方法是定义商为任意整数,余数为被除数
为除数(Divisor)。如果除数为0,那么一种方法是定义商为任意整数,余数为被除数 、
、 为整数
为整数
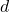 满足
满足![Rendered by QuickLaTeX.com \[ d | a,\; d | b, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7be188addd195a0e39e4a30262d613ec_l3.png)
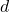 称为
称为 、
、 的公因子,并且最大公因子(Greatest Common Divisor,GCD)记为
的公因子,并且最大公因子(Greatest Common Divisor,GCD)记为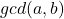
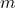 满足
满足![Rendered by QuickLaTeX.com \[ a | m,\; b | m, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e67cadfc4849b01b4cbb194f0c46a4c4_l3.png)
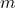 称为
称为 、
、 的公倍数,并且最小公倍数(Least Common Multiple,LCM)记为
的公倍数,并且最小公倍数(Least Common Multiple,LCM)记为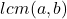
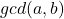 。利用带余除法,
。利用带余除法,![Rendered by QuickLaTeX.com \[ gcd(a, b) = gcd(a - qb, b) = gcd(b, r), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fe5402151f379b761cc8a2f06552c795_l3.png)
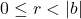 。再次利用带余除法,
。再次利用带余除法,![Rendered by QuickLaTeX.com \[ gcd(b, r) = gcd(b - q'r, r) = gcd(r, r'), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-96470169241c6084f5249075289496ee_l3.png)
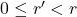 。因此,除数会递减至0,并且剩下的被除数会等于
。因此,除数会递减至0,并且剩下的被除数会等于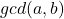
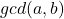 )都具有
)都具有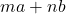 的形式。因此,我们可以得到Bézout定理
的形式。因此,我们可以得到Bézout定理![Rendered by QuickLaTeX.com \[ gcd(a, b) = ma + nb \text{ for some } m, n \in \mathbb{Z}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a760a37d3721719ddbd73215867606dc_l3.png)
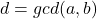 、
、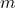 、
、
![Rendered by QuickLaTeX.com \[ a_1 = a,\; b_1 = b. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-006882d971ecb98751b89f98af8a2963_l3.png)
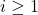 ,令
,令![Rendered by QuickLaTeX.com \[ a_{i + 1} = b_i,\; b_{i + 1} = r_i, \text{ where } a_i = q_ib_i + r_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-362b547213b89f761a197e8c07ce4705_l3.png)
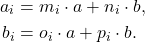
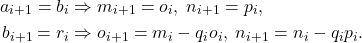
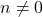 ,我们有素因子分解(Prime Factorization)
,我们有素因子分解(Prime Factorization)![Rendered by QuickLaTeX.com \[ n = u \cdot p_1 \cdots p_k, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5b8da2d94145d88b132a125302b62553_l3.png)
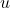 为单位,
为单位,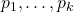 为素数
为素数
 是正整数(或者负整数),那么
是正整数(或者负整数),那么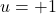 (或者
(或者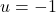 )。因此,从下面开始,我们通常只考虑正整数的情形
)。因此,从下面开始,我们通常只考虑正整数的情形 是素数,那么它不能继续进行分解。如果
是素数,那么它不能继续进行分解。如果 不是素数,那么
不是素数,那么![Rendered by QuickLaTeX.com \[ n = ab,\; 1 < a \leq b < n, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-84ead6ae91badc3bb58567c9c1614445_l3.png)
 、
、 可以递归地进行分解,直到不能继续进行分解
可以递归地进行分解,直到不能继续进行分解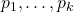 为所有素数。考虑
为所有素数。考虑![Rendered by QuickLaTeX.com \[ n = p_1 \cdots p_k + 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-83ab51cad5c0798215d4eee7b588a571_l3.png)
![Rendered by QuickLaTeX.com \[ n = p_1 \cdots p_k + 1 = p_{i_1} \cdots p_{i_l}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8ab8a256bb1165fbc0224cca9d9d5812_l3.png)
 ,矛盾
,矛盾![Rendered by QuickLaTeX.com \[ n = u \cdot \prod_i p_i^{k_i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-68e11da60b317023fa5c9238d50ef678_l3.png)
 、
、 用相同的素因子来表示(缺少的素因子指数为0),
用相同的素因子来表示(缺少的素因子指数为0),![Rendered by QuickLaTeX.com \[ a = \prod_i p_i^{k_i},\; b = \prod_i p_i^{l_i}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-44ec5e0253fcac1a14546bdad80490a5_l3.png)
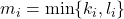 、
、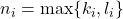 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ gcd(a, b) = \prod_i p_i^{m_i},\; lcm(a, b) = \prod_i p_i^{n_i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1c1f6f35b8d5cba9fa780f6baa9648b4_l3.png)
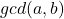 之后,我们可以利用如下关系找到
之后,我们可以利用如下关系找到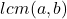
![Rendered by QuickLaTeX.com \[ m_i + n_i = k_i + l_i \Rightarrow gcd(a, b) \cdot lcm(a, b) = ab. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a71e427c4c6f8723176a27f245f95e18_l3.png)
 的所有素数。一种方法是Eratosthenes筛法(Sieve)
的所有素数。一种方法是Eratosthenes筛法(Sieve)
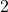 到
到 的列表
的列表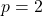 。从列表中去掉
。从列表中去掉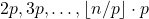
 的最小正整数。将它赋值给
的最小正整数。将它赋值给 ,并且重复上述过程
,并且重复上述过程 的正整数,那么列表包含了不大于
的正整数,那么列表包含了不大于 的所有素数
的所有素数![Rendered by QuickLaTeX.com \[ \pi(n) \sim \frac{n}{\ln n} \text{ as } n \to \infty, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d437333368660e58814c51c891af72a6_l3.png)
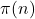 是不大于
是不大于 的所有素数的个数
的所有素数的个数