基本的矩阵群
- 在从线性方程出发中,我们有可逆矩阵。在数值线性代数中,我们有正交矩阵、酉矩阵
- 设
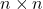 矩阵的集合为
矩阵的集合为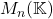 ,其中
,其中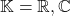
- 可逆矩阵的集合为一般线性群
进一步,令行列式为1,可得特殊线性群![Rendered by QuickLaTeX.com \[ GL_n(\mathbb{K}) = \{ g \in M_n(\mathbb{K}) : \det(g) \neq 0 \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a3deefc6136e05e0ed00ae0dd508a64b_l3.png)
![Rendered by QuickLaTeX.com \[ SL_n(\mathbb{K}) = \{ g \in M_n(\mathbb{K}) : \det(g) = 1 \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b2782acd170a29c45038ecafa87016e4_l3.png)
- 正交矩阵的集合为正交群
进一步,令行列式为1,可得特殊正交群![Rendered by QuickLaTeX.com \[ O_n(\mathbb{K}) = \{ g \in M_n(\mathbb{K}) : gg^T = I \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4e3bc9093de12276eee09c93464d3311_l3.png)
![Rendered by QuickLaTeX.com \[ SO_n(\mathbb{K}) = \{ g \in M_n(\mathbb{K}) : gg^T = I,\; \det(g) = 1 \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c02c3581ed65856286d6f0b4dc5b7808_l3.png)
- 酉矩阵的集合为酉群
进一步,令行列式为1,可得特殊酉群![Rendered by QuickLaTeX.com \[ U_n(\mathbb{K}) = \{ g \in M_n(\mathbb{K}) : gg^* = I \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1c38a35dc7d20a90c5a4d3228089ae9e_l3.png)
![Rendered by QuickLaTeX.com \[ SU_n(\mathbb{K}) = \{ g \in M_n(\mathbb{K}) : gg^* = I,\; \det(g) = 1 \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9eff3b80456d9e6a1dbe165888a8051f_l3.png)
- 可逆矩阵的集合为一般线性群
- 矩阵群之间的关系
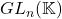 、
、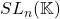 的行列式相差的倍数为
的行列式相差的倍数为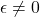 ,故
,故
其中,商群的等价类为![Rendered by QuickLaTeX.com \[ GL_n(\mathbb{K}) / SL_n(\mathbb{K}) \cong \mathbb{K} - \{ 0 \}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bd798f000366eecadaee07d6c16f8172_l3.png)
![Rendered by QuickLaTeX.com \[ g \cdot SL_n(\mathbb{K}), \text{ where } g = \begin{bmatrix}\epsilon & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1\end{bmatrix},\; \epsilon \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-78f58a1870a77fe9ca0a0be754fd4f00_l3.png)
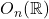 、
、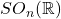 的行列式相差的倍数为
的行列式相差的倍数为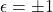 ,故
,故
其中,商群的等价类为![Rendered by QuickLaTeX.com \[ O_n(\mathbb{R}) / SO_n(\mathbb{R}) \cong \mathbb{Z}_2, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-998582a96e2856faf0faa8e2f9c4baa6_l3.png)
![Rendered by QuickLaTeX.com \[ g \cdot SO_n(\mathbb{R}), \text{ where } g = \begin{bmatrix}\epsilon & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1\end{bmatrix},\; \epsilon = \pm 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dcfbc236391c12aca2f39ff9cca64734_l3.png)
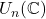 、
、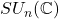 的行列式相差的倍数为
的行列式相差的倍数为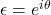 ,故
,故
其中,商群的等价类为![Rendered by QuickLaTeX.com \[ U_n(\mathbb{C}) / SU_n(\mathbb{C}) \cong S^1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4c67c3a99f6715dc4b51863ecf26a60d_l3.png)
![Rendered by QuickLaTeX.com \[ g \cdot SU_n(\mathbb{C}), \text{ where } g = \begin{bmatrix}\epsilon & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1\end{bmatrix},\; \epsilon = e^{i\theta}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9ec842e88a602bcdc6a7bd4a1fb42b86_l3.png)
- 上面的群有些是重复的,
不过,![Rendered by QuickLaTeX.com \[ O_n(\mathbb{R}) = U_n(\mathbb{R}),\; SO_n(\mathbb{R}) = SU_n(\mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-536b8528bc1e7006906b4b2aebdf5311_l3.png)
在不同的地方,矩阵群的记号有不同的形式,比如![Rendered by QuickLaTeX.com \[ O_n(\mathbb{C}) \neq U_n(\mathbb{C}),\; SO_n(\mathbb{C}) \neq SU_n(\mathbb{C}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c4bcc14a4858610021f38f27c65ccaff_l3.png)
![Rendered by QuickLaTeX.com \[ O_n(\mathbb{R}) = O(n, \mathbb{R}) = O(n),\; SO_n(\mathbb{R}) = SO(n, \mathbb{R}) = SO(n), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6246f1951802f39790f94284c7bca3f6_l3.png)
![Rendered by QuickLaTeX.com \[ U_n(\mathbb{C}) = U(n, \mathbb{C}) = U(n),\; SU_n(\mathbb{C}) = SU(n, \mathbb{C}) = SU(n). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7680cd6a35cd5526f917372f644a23b3_l3.png)
保持形式的群
- 在数值线性代数中,我们有双线性形式、内积、实对称矩阵、Hermite矩阵
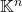 上的双线性形式为
上的双线性形式为![Rendered by QuickLaTeX.com \[ \beta(x, y) = x^TBy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e4e6133a2842f848e7725782d58d38b_l3.png)
- 更换一组基底对应于合同变换,
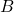 可以化归为对角矩阵
可以化归为对角矩阵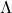
- 在复数域上,我们可以对复数开平方根,所以
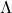 的元素可以化归为0、1(在实数域上,我们只能对非负实数开平方根,所以
的元素可以化归为0、1(在实数域上,我们只能对非负实数开平方根,所以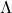 的元素可以化归为0、1、-1。只包含1 –> 正定,只包含1、0 –> 半正定,只包含-1 –> 负定,只包含-1、0 –> 半负定,同时包含1、-1 –> 不定)
的元素可以化归为0、1、-1。只包含1 –> 正定,只包含1、0 –> 半正定,只包含-1 –> 负定,只包含-1、0 –> 半负定,同时包含1、-1 –> 不定)
- 更换一组基底对应于合同变换,
- 保持双线性形式(对应的二次型)的群为
![Rendered by QuickLaTeX.com \[ Aut(\mathbb{K}^n, \beta) = \{ g \in GL_n(\mathbb{K}) : g^TBg = B \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-044b5f244a633e9305c8b55e55ec84be_l3.png)
- (对称)不定正交群为
![Rendered by QuickLaTeX.com \[ O_{p, q}(\mathbb{K}) = Aut(\mathbb{K}^{p + q}, \beta),\; B = \begin{bmatrix}I_p & 0 \\ 0 & -I_q\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-50282b699fc45d461a61b37302b7015f_l3.png)
- (反对称)辛群为
![Rendered by QuickLaTeX.com \[ Sp_{2n}(\mathbb{K}) = Aut(\mathbb{K}^{2n}, \beta),\; B = \begin{bmatrix}0 & I_n \\ -I_n & 0\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-188b7b7ddb4a87ae7b692e0037f7522f_l3.png)
- (对称)不定正交群为
- 类似于双线性形式,我们也可以考虑内积。此时,
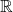 、
、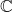 的情形是不同的
的情形是不同的
- (双线性)
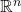 上的内积为
上的内积为![Rendered by QuickLaTeX.com \[ \langle{x, y}\rangle_{\mathbb{R}^n} = x^Ty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-481441c8646c1b1fcc5d47f43246ea87_l3.png)
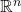 上的对称、双线性形式对应于实对称矩阵
上的对称、双线性形式对应于实对称矩阵
因为![Rendered by QuickLaTeX.com \[ \beta(x, y) = x^TBy, \text{ where } B^T = B. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3346b9e9a97947ae667a9df616b09ecd_l3.png)
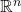 上的内积是双线性形式,所以保持对称、双线性形式(对应的二次型)的群化归为上面的情形
上的内积是双线性形式,所以保持对称、双线性形式(对应的二次型)的群化归为上面的情形 - (线性-共轭线性)
 上的内积为
上的内积为![Rendered by QuickLaTeX.com \[ \langle{x, y}\rangle_{\mathbb{C}^n} = x^T\overline{y}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-054e7201f36e6056658e4838580bf175_l3.png)
 上的Hermite形式对应于Hermite矩阵
上的Hermite形式对应于Hermite矩阵
因为![Rendered by QuickLaTeX.com \[ \beta(x, y) = x^TB\overline{y}, \text{ where } B^* = B. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c10e895a6189755049287c5cc6178a73_l3.png)
 上的内积不是双线性形式,所以我们需要考虑保持Hermite形式(对应的共轭二次型)的群
上的内积不是双线性形式,所以我们需要考虑保持Hermite形式(对应的共轭二次型)的群
不定酉群为![Rendered by QuickLaTeX.com \[ Aut(\mathbb{C}^n, \beta) = \{ g \in GL_n(\mathbb{C}) : g^TB\overline{g} = B \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-60502edae6436bbc16a64a767bd0151d_l3.png)
![Rendered by QuickLaTeX.com \[ U_{p, q}(\mathbb{C}) = Aut(\mathbb{C}^{p + q}, \beta),\; B = \begin{bmatrix}I_p & 0 \\ 0 & -I_q\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3a52dda2607408455115f28b2cbfae9b_l3.png)
- (双线性)
半直积构成的群
- 设
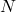 、
、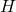 为群,
为群,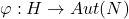 为群同态
为群同态
- 半直积
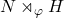 上的乘法定义为
上的乘法定义为![Rendered by QuickLaTeX.com \[ (n, h) \cdot (n', h') = (n \cdot \varphi(h)n', h \cdot h'),\; n, n' \in N,\; h, h' \in H. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c88eae0df462db67f54ab0c6c8c0b285_l3.png)
- 群同态
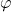 等价于
等价于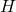 在
在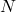 上的左作用,所以我们通常可以省略
上的左作用,所以我们通常可以省略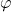
- 半直积
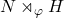 关于乘法构成一个群
关于乘法构成一个群
- 单位元为
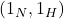 。逆元由如下等式得到,
。逆元由如下等式得到,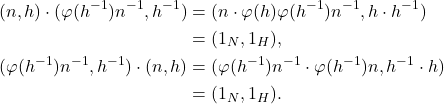
- 结合律由如下等式得到,
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} &\mathrel{\phantom{=}} [(n_1, h_1) \cdot (n_2, h_2)] \cdot (n_3, h_3) \\ &= (n_1 \cdot \varphi(h_1)n_2, h_1 \cdot h_2) \cdot (n_3, h_3) \\ &= (n_1 \cdot \varphi(h_1)n_2 \cdot \varphi(h_1 \cdot h_2)n_3, h_1 \cdot h_2 \cdot h_3) \\ &= (n_1 \cdot \varphi(h_1)[n_2 \cdot \varphi(h_2)n_3], h_1 \cdot h_2 \cdot h_3) \\ &= (n_1, h_1) \cdot (n_2 \cdot \varphi(h_2)n_3, h_2 \cdot h_3) \\ &= (n_1, h_1) \cdot [(n_2, h_2) \cdot (n_3, h_3)]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-eb621aaacd960285a0f27ed393e813d3_l3.png)
- 单位元为
- 在计算机图形学中,我们有仿射变换、刚体变换。可参见计算机图形学的几何变换
- 仿射变换为
仿射变换的复合为![Rendered by QuickLaTeX.com \[ f(x) = Ax + b,\; A \in GL_n(\mathbb{R}),\; b \in \mathbb{R}^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e57d300beee1db7b314ae43e3ec61e0c_l3.png)
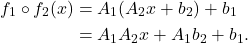
- 因此,仿射变换群为
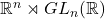 ,其中
,其中
也就是说,仿射变换群可以分解为一个平移部分、一个可逆的线性变换部分![Rendered by QuickLaTeX.com \[ (b_1, A_1) \cdot (b_2, A_2) = (b_1 + A_1b_2, A_1A_2). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6646a8fcae2e8fa6daa29502e08685f7_l3.png)
- 类似地,Euclid群为
进一步,刚体变换群为特殊Euclid群![Rendered by QuickLaTeX.com \[ E_n(\mathbb{R}) = \mathbb{R}^n \rtimes O_n(\mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dbc691402597cbca642683925b6bf636_l3.png)
![Rendered by QuickLaTeX.com \[ SE_n(\mathbb{R}) = \mathbb{R}^n \rtimes SO_n(\mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-282c453b80948aae06cda6742bb3e931_l3.png)
- 仿射变换为
- 在经典力学中,我们有Galileo变换;在狭义相对论中,我们有Poincaré变换。可参见Lagrange力学
- 经典力学中的Galileo变换
- 如果坐标系更换一组单位正交基,那么物理规律不变,对应的Galileo变换为
如果坐标系相对于另一个坐标系作匀速直线运动,那么物理规律不变,对应的Galileo变换为![Rendered by QuickLaTeX.com \[ f(r, t) = (Rr, t),\; R \in O_3(\mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0a6ee0de61a1ebbb02e79f4170bf5d75_l3.png)
考虑上述2种Galileo变换,变换的复合为![Rendered by QuickLaTeX.com \[ f(r, t) = (r + vt, t),\; v \in \mathbb{R}^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e64ede32a0497f5eb2040e2d9f6c5175_l3.png)
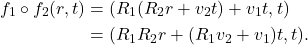
- 因此,在Galileo变换群中,可逆的线性变换部分为Euclid群
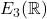 。如果再加上空间平移、时间平移
。如果再加上空间平移、时间平移
那么Galileo变换群为![Rendered by QuickLaTeX.com \[ f(r, t) = (r + r_0, t + t_0),\; r_0 \in \mathbb{R}^3,\; t_0 \in \mathbb{R}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b87fab3a55cc432def13d5e999bebe6c_l3.png)
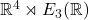
- 如果坐标系更换一组单位正交基,那么物理规律不变,对应的Galileo变换为
- 狭义相对论中的Poincaré变换
- 光速不变的方程为(假设光速为1)
这是一个对称、双线性形式(对应的二次型),Poincaré变换保持它不变![Rendered by QuickLaTeX.com \[ dr^2 - dt^2 = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7085f471ce1945b4027700b37e89180e_l3.png)
- 因此,在Poincaré变换群中,可逆的线性变换部分为Lorentz群
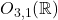 。如果再加上空间平移、时间平移,那么Poincaré变换群为
。如果再加上空间平移、时间平移,那么Poincaré变换群为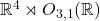
- 光速不变的方程为(假设光速为1)
- 由上述可知,物理规律和对称性有关,并且对称性可以用群来刻画。在经典力学中,Galileo变换群对应的空间、时间是独立的;在狭义相对论中,Poincaré变换群对应的空间、时间是不独立的
- 经典力学中的Galileo变换