有限域
- 设
 为有限域。那么,我们有环同态
为有限域。那么,我们有环同态
因此,我们有环嵌入![Rendered by QuickLaTeX.com \[ f: \mathbb{Z} \to F,\; n \to n1_F. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-91669c31423b8db89575760485488580_l3.png)
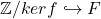 ,从而
,从而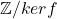 为整环(
为整环( 中没有零因子)。由此可知,
中没有零因子)。由此可知,
其中,![Rendered by QuickLaTeX.com \[ kerf = p\mathbb{Z},\; \mathbb{Z} / kerf = \mathbb{Z} / p\mathbb{Z} = \mathbb{F}_p, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e4f0665a020c61ad4e12dc9d9df6e9a1_l3.png)
 为素数,
为素数,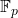 为
为 阶有限域
阶有限域 - 我们也称
 的特征为
的特征为 ,记为
,记为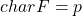 。也就是说,在特征为
。也就是说,在特征为 的域中,
的域中, 的倍数等于0
的倍数等于0 - 对于域扩张
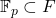 ,设
,设![Rendered by QuickLaTeX.com [F : \mathbb{F}_p] = r](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7e9a4c88598b6aaa8ab3d5aaaa05c9a8_l3.png) 。那么,
。那么, 中的元素可以表示为
中的元素可以表示为
其中,![Rendered by QuickLaTeX.com \[ x_1e_1 + \cdots + x_re_r,\; x_i \in \mathbb{F}_p, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c2f875fbbed9be958343ff1d6def65f7_l3.png)
 为
为 的一组
的一组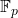 -基底。因此,
-基底。因此,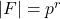
存在性和唯一性
- 由上面的笔记可知,有限域的阶为
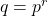 。反过来,对任意
。反过来,对任意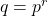 ,存在一个有限域,它的阶为
,存在一个有限域,它的阶为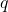
- 我们取
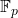 的代数闭包
的代数闭包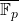 ,然后考察如下多项式的所有零点,
,然后考察如下多项式的所有零点,![Rendered by QuickLaTeX.com \[ P(X) = X^q - X \in \mathbb{F}_p[X]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a99f79b9d05610887af7389c521a96d3_l3.png)
- 由于
故![Rendered by QuickLaTeX.com \[ (P, P') = (X^q - X, qX^{q - 1} - 1) = (X^q - X, -1) = 1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5d649a8acd38c6df0df69bb946ba9d17_l3.png)
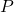 没有重因式,我们可以得到
没有重因式,我们可以得到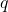 个不同的零点
个不同的零点![Rendered by QuickLaTeX.com \[ F = \{ \alpha_1, \ldots, \alpha_q \} \subset \overline{\mathbb{F}_p}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-499ffa305101f7c7ca316611b9bd578f_l3.png)
- 我们只需证明
 为一个域,下面以加法为例(减法、乘法、除法是类似的)。注意到
为一个域,下面以加法为例(减法、乘法、除法是类似的)。注意到
这里,我们用到了![Rendered by QuickLaTeX.com \[ (\alpha_i + \alpha_j)^p = \alpha_i^p + \alpha_j^p. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b2ccfad784dd057f1ab4673df4666d1f_l3.png)
 整除二项式系数
整除二项式系数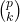 ,
,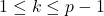 。迭代
。迭代 次,可得
次,可得
因此,![Rendered by QuickLaTeX.com \[ (\alpha_i + \alpha_j)^q = \alpha_i^q + \alpha_j^q = \alpha_i + \alpha_j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-142f4f6a4858f4ed07ef163ed03a501e_l3.png)
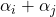 也是
也是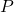 的零点,
的零点, 在加法下封闭
在加法下封闭
- 我们取
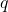 阶有限域是唯一的,记为
阶有限域是唯一的,记为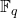 ,它也叫做Galois域
,它也叫做Galois域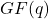
- 设
 为
为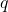 阶有限域。那么,
阶有限域。那么,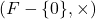 为一个群。由Lagrange定理可知,
为一个群。由Lagrange定理可知,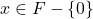 生成的子群的阶整除
生成的子群的阶整除 ,从而
,从而![Rendered by QuickLaTeX.com \[ x^{q - 1} = 1,\; x \in F - \{ 0 \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e2a87d42032612f03d88f4ee6902eb62_l3.png)
- 也就是说,
 的所有元素为
的所有元素为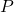 的所有零点,这对应于分裂域。分裂域在同构的意义下是唯一的,上面构造的是分裂域的一个实例
的所有零点,这对应于分裂域。分裂域在同构的意义下是唯一的,上面构造的是分裂域的一个实例
- 设