什么是线性
- 根据Gauss消元法,我们认为如下运算是线性的
- (域)系数可以进行加法、减法、乘法、除法,这对应于域
- (Abel群)不同的行可以进行加法,这对应于Abel群
- 除此之外,域上的运算、Abel群上的运算应该是相容的
- (域的加法,关于Abel群)
![Rendered by QuickLaTeX.com \[ (\lambda_1 + \lambda_2)v = \lambda_1v + \lambda_2v. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d5d927344fc73c87d7fe99056117f99b_l3.png)
- (域的乘法,关于Abel群)
![Rendered by QuickLaTeX.com \[ (\lambda_1\lambda_2)v = \lambda_1(\lambda_2v). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e6faab4e29cf017987a3adf1d44a07aa_l3.png)
- (Abel群的加法,关于域)
![Rendered by QuickLaTeX.com \[ \lambda(v_1 + v_2) = \lambda v_1 + \lambda v_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2ee76707c79cd76f7008a217e51b9451_l3.png)
- 在域中,减法为加法的逆运算,除法为乘法的逆运算。因此,我们只考虑了加法、乘法,并且域也可以减弱为环(有单位元素
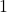 的交换环),满足
的交换环),满足![Rendered by QuickLaTeX.com \[ 1v = v. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b5c0e00b20ecc26aed61fe8288b5cd03_l3.png)
- 加法的相容性,也叫做分配律。在左右两边,加法满足分配律,这对应于
- (域的加法,关于Abel群)
- Abel范畴、模范畴
- 域(Field)、Abel群经过
 ,可以得到向量空间(Vector Space)
,可以得到向量空间(Vector Space)![Rendered by QuickLaTeX.com \[ V = F \otimes A. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5ce9e9a7cad8471e99b79e34540a1ab2_l3.png)
- 环(Ring)、Abel群经过
 ,可以得到模(Module)
,可以得到模(Module)![Rendered by QuickLaTeX.com \[ M = R \otimes A. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-caf3ee07d4d7fc8a941aa946c2a951e4_l3.png)
- Abel群、环、域、模、向量空间,它们都是Abel群,所以它们都可以在Abel范畴中讨论。在Abel范畴中,我们可以定义核
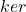 、像
、像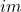 ,可参见Abel范畴和导出函子
,可参见Abel范畴和导出函子
- Abel群 –> 加法
- 环 –> 加法、乘法
- 域 –> 加法、减法、乘法、除法
- 模 –> 系数为环,加法
- 向量空间 –> 系数为域,加法
- Abel群也是
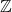 -模,所以它们也可以在模范畴中讨论。在模范畴中,我们可以定义
-模,所以它们也可以在模范畴中讨论。在模范畴中,我们可以定义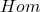 、
、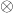 ,可参见模范畴和同态函子、张量积函子
,可参见模范畴和同态函子、张量积函子 - 矩阵的集合既是环(乘法为矩阵的乘法),也是
 -向量空间,我们称这样的空间为
-向量空间,我们称这样的空间为 -代数。因此,矩阵代数为有单位元素的、结合的、非交换的
-代数。因此,矩阵代数为有单位元素的、结合的、非交换的 -代数。
-代数。
- 注意,环的乘法是结合的,而代数的乘法不一定是结合的,比如Lie代数(乘法为Poisson括号)不是结合的,我们有Jacobi恒等式
- 域(Field)、Abel群经过
从线性空间到张量
- 向量空间中的元素称为向量,向量空间也叫作线性空间
- 在求解线性方程时,如果某些行乘以常数倍相加等于另一行,那么有一部分方程不是独立的
- 类似地,如果存在不全为0的
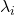 ,使得
,使得
那么![Rendered by QuickLaTeX.com \[ \sum_{i = 1}^n \lambda_iv_i = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f5671b5e4b10c476c97ce776b5f21490_l3.png)
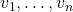 称为线性相关的,此时某些向量乘以常数倍相加等于另一个向量
称为线性相关的,此时某些向量乘以常数倍相加等于另一个向量 - 因此,所有独立的方程,对应于数量最多的线性无关的向量组,它称为极大线性无关组,其数量称为秩。在线性空间中,数量最多的线性无关的向量组也叫做基底,其数量也叫做维数
- 设
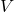 为
为 维
维 -线性空间,
-线性空间,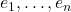 为
为 -基底
-基底
- (基底是线性无关的)我们有
![Rendered by QuickLaTeX.com \[ \sum_{i = 1}^n \lambda_ie_i = 0 \Rightarrow \lambda_i = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b8c4ef2904ca5fa3ad015fc6988f0b71_l3.png)
- (基底可以生成线性空间)对任意
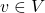 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ \sum_{i = 1}^n \lambda_ie_i = v,\; \lambda_i \in F. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4a82dcc6bc07a5de80bc1088e763dfb2_l3.png)
- 在固定一组
 -基底后,
-基底后,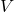 可以等同于
可以等同于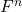 。我们也将维数记为
。我们也将维数记为![Rendered by QuickLaTeX.com \[ n = dim_FV. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-87d5c2b4c19bad03fe05fb8a1e637fc0_l3.png)
- 线性映射
 为保持加法、系数的映射,
为保持加法、系数的映射,
在固定一组![Rendered by QuickLaTeX.com \[ f(v_1 + v_2) = f(v_1) + f(v_2),\; f(\lambda v) = \lambda f(v). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-67bc0709aa3e5d35d65b6e37c0afb50c_l3.png)
 -基底后,对任意
-基底后,对任意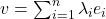 ,我们有
,我们有
因此,![Rendered by QuickLaTeX.com \[ f(v) = \sum_{i = 1}^n \lambda_if(e_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-51eb064289a11b81f204a6591cecd555_l3.png)
 只需指定在基底上的值,即可线性扩张为
只需指定在基底上的值,即可线性扩张为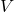 上的线性映射
上的线性映射
- (基底是线性无关的)我们有
- 所有线性映射
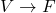 构成一个线性空间,称为对偶线性空间
构成一个线性空间,称为对偶线性空间![Rendered by QuickLaTeX.com \[ V^* = Hom(V, F). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cdb9cb4f203973d58459a0138913195d_l3.png)
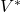 的对偶基底
的对偶基底 满足
满足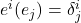 ,它们可以线性扩张为
,它们可以线性扩张为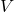 上的线性映射,
上的线性映射,![Rendered by QuickLaTeX.com \[ e^i(v) = \sum_{j = 1}^n \lambda_je^i(e_j) = \lambda_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b0d70f5389a161021810563e43792b2b_l3.png)
- (
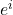 是线性无关的)如果
是线性无关的)如果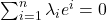 ,那么将其作用于
,那么将其作用于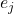 ,可得
,可得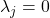
- (
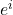 可以生成
可以生成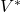 )对任意
)对任意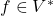 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ f = \sum_{i = 1}^n f(e_i) \cdot e^i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f1d70a1e1e5202830542a83489ffff49_l3.png)
- 线性映射
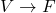 即线性函数,通常记为配对
即线性函数,通常记为配对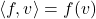 ,故
,故![Rendered by QuickLaTeX.com \[ f = \sum_{i = 1}^n \langle{f, e_i}\rangle \cdot e^i,\; f \in V^*. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cdb6078bfc86ecf0ffd26e2163e3b249_l3.png)
- (
- 双线性形式
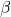 对两个分量都是线性的,即对于任意固定的
对两个分量都是线性的,即对于任意固定的 、
、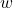 ,
,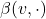 、
、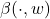 都为线性映射
都为线性映射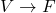 。在左右两边,双线性形式的加法满足分配律,这对应于
。在左右两边,双线性形式的加法满足分配律,这对应于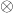 。因此,类似于线性映射的情形,我们有
。因此,类似于线性映射的情形,我们有
所有双线性形式![Rendered by QuickLaTeX.com \[ e^i(v)e^j(w) = (e^i \otimes e^j)(v, w),\; \beta = \sum_{i, j = 1}^n \beta(e_i, e_j)e^i \otimes e^j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6df5fe1ec5b3317a2457e5b0f42741bb_l3.png)
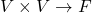 构成一个线性空间
构成一个线性空间![Rendered by QuickLaTeX.com \[ V^* \otimes V^*. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2ca284be61c8e2d61e0c7d79afe358a4_l3.png)
- 现在,利用
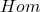 、
、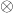 ,我们可以构造一般的张量空间
,我们可以构造一般的张量空间
如果![Rendered by QuickLaTeX.com \[ V \otimes \cdots \otimes V \otimes V^* \otimes \cdots \otimes V^*. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3f7fcf7a849bb62a88ce41f099cc050b_l3.png)
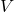 的数量为
的数量为 、
、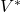 的数量为
的数量为 ,那么其中的元素称为
,那么其中的元素称为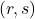 -型张量。张量的集合既是环(乘法为
-型张量。张量的集合既是环(乘法为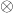 ),也是
),也是 -向量空间,故我们可以得到张量代数
-向量空间,故我们可以得到张量代数
- 在数值计算中,我们通常固定一组
 -基底。此时,
-基底。此时,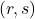 -型张量可以等同于
-型张量可以等同于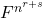 中的元素,即
中的元素,即 上的
上的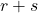 维数组
维数组 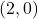 -型、
-型、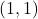 -型、
-型、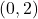 -型张量可以等同于
-型张量可以等同于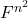 中的元素,即
中的元素,即 上的矩阵,这是在数值计算中最常见的情形
上的矩阵,这是在数值计算中最常见的情形
- 在数值计算中,我们通常固定一组
矩阵的更多性质
- 我们考虑最常见的情形,即矩阵。同时,我们考虑复数域,故我们可以使用Cauchy积分定理、Cauchy积分公式、代数基本定理。关于复数域,可参见复数域上的分析
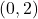 -型张量即双线性形式
-型张量即双线性形式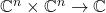 ,
,
它对应于一个二次型![Rendered by QuickLaTeX.com \[ \beta(x, y) = x^TBy = \sum_{i, j = 1}^n b_{ij}x_iy_j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0abdd37b8060885df03daf391617e899_l3.png)
![Rendered by QuickLaTeX.com \[ \beta(x, x) = x^TBx = \sum_{i, j = 1}^n b_{ij}x_ix_j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b9480196a5b979ca871fa1adc04c0bf0_l3.png)
- 我们可以使用配方法,将二次型转化为平方和(平方项可以带系数)。这等价于存在一个可逆矩阵
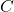 、一个对角矩阵
、一个对角矩阵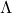 ,使得
,使得
即![Rendered by QuickLaTeX.com \[ y = Cx,\; x^TBx = y^T\Lambda y. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-97227353dd22fd81cae153f8b881b075_l3.png)
因此,关于矩阵![Rendered by QuickLaTeX.com \[ (C^{-1})^TBC^{-1} = \Lambda. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-016531eb967d07fe592c08461c4a2360_l3.png)
 的变换为
的变换为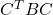 (将
(将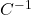 重命名为
重命名为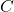 ),它称为合同变换
),它称为合同变换
- 我们可以使用配方法,将二次型转化为平方和(平方项可以带系数)。这等价于存在一个可逆矩阵
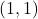 -型张量即线性变换
-型张量即线性变换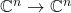 ,
,
线性变换![Rendered by QuickLaTeX.com \[ f = \sum_{i, j = 1}^n a_{ij}e_j \otimes e^i,\; f(e_i) = \sum_{j = 1}^n a_{ij}e_j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b5f9321fcaf411e838f398b2e39f627b_l3.png)
 的矩阵为
的矩阵为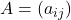 ,我们有
,我们有
如果我们更换一组基底,那么![Rendered by QuickLaTeX.com \[ \begin{bmatrix}f(e_1) \\ \vdots \\ f(e_n)\end{bmatrix} = \begin{bmatrix}a_{11} & \ldots & a_{1n} \\ \vdots & & \vdots \\ a_{n1} & \ldots & a_{nn} \end{bmatrix} \cdot \begin{bmatrix}e_1 \\ \vdots \\ e_n\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-768d87552b87fc04eb35e1102494c565_l3.png)
因此,关于矩阵![Rendered by QuickLaTeX.com \[ \begin{bmatrix}c_{11} & \ldots & c_{1n} \\ \vdots & & \vdots \\ c_{n1} & \ldots & c_{nn}\end{bmatrix} \cdot \begin{bmatrix}f(e_1') \\ \vdots \\ f(e_n')\end{bmatrix} = \begin{bmatrix}a_{11} & \ldots & a_{1n} \\ \vdots & & \vdots \\ a_{n1} & \ldots & a_{nn}\end{bmatrix} \cdot \begin{bmatrix}c_{11} & \ldots & c_{1n} \\ \vdots & & \vdots \\ c_{n1} & \ldots & c_{nn}\end{bmatrix} \cdot \begin{bmatrix}e_1' \\ \vdots \\ e_n'\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-adcf66888f7227d00845b9af8ef89cfc_l3.png)
 的变换为
的变换为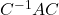 ,它称为相似变换
,它称为相似变换
- (核、像)线性变换对应于矩阵,反过来,矩阵也对应于线性变换(即线性算子)。矩阵
 的核
的核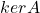 、像
、像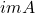 为
为 的子空间。如果取
的子空间。如果取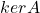 的一组基底
的一组基底 ,然后扩充为
,然后扩充为 的一组基底
的一组基底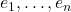 ,那么
,那么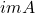 的一组基底为
的一组基底为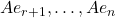 ,从而
,从而
商空间![Rendered by QuickLaTeX.com \[ dimkerA + dimimA = n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7a7ce13c6b210514d86eae26cd73f16c_l3.png)
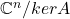 的一组基底为
的一组基底为![Rendered by QuickLaTeX.com [e_{r + 1}], \ldots, [e_n]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9e116baf09b7a78ba01524373dd686e5_l3.png) ,故我们有同构定理
,故我们有同构定理![Rendered by QuickLaTeX.com \[ \mathbb{C}^n / kerA \cong imA. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-436ee0b1f4edca741748563b50383d08_l3.png)
- (矩阵乘积的核)对于矩阵乘积的核
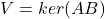 ,取线性映射
,取线性映射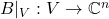 ,我们有
,我们有
注意到![Rendered by QuickLaTeX.com \[ dimkerB|_V + dimimB|_V = dimV. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6e1080dd71586a4fdb767de2a5a07a4d_l3.png)
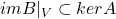 ,故
,故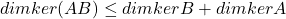 。利用数学归纳法,
。利用数学归纳法,![Rendered by QuickLaTeX.com \[ dimker\prod_i A_i \leq \sum_i dimkerA_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-26742f8d4ba39bacd6968c1c34b07e01_l3.png)
- (直和)对于子空间
 ,如果
,如果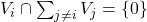 ,那么子空间之间的向量是线性无关的,它们可以构成直和
,那么子空间之间的向量是线性无关的,它们可以构成直和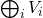 。由于
。由于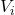 的基底可以合成为
的基底可以合成为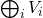 的基底,故
的基底,故![Rendered by QuickLaTeX.com \[ dim\bigoplus_i V_i = \sum_i dimV_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8ac3f2a1a4712ad5536b65669b07fb7d_l3.png)
- (核、像)线性变换对应于矩阵,反过来,矩阵也对应于线性变换(即线性算子)。矩阵
- 类似于合同变换,我们考虑相似变换的对角化问题
因为矩阵的乘法为左边的行、乘以右边的列,所以我们可以对矩阵进行分块,然后进行乘法。比如,对于列向量的分块![Rendered by QuickLaTeX.com \[ C^{-1}AC = \Lambda. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e603b8bbfdb07ea0725e8f55fc6b7051_l3.png)
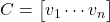 ,我们有
,我们有
因此,![Rendered by QuickLaTeX.com \[ A \cdot \begin{bmatrix}v_1 \cdots v_n\end{bmatrix} = \begin{bmatrix}v_1 \cdots v_n\end{bmatrix} \cdot \begin{bmatrix}\lambda_1 & & \\ & \ddots \\ & & \lambda_n\end{bmatrix} = \begin{bmatrix}\lambda_1v_1 \cdots \lambda_nv_n\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e67ff98eba2c0ba4c6b6aabdfc731b71_l3.png)
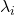 、
、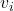 满足如下方程
满足如下方程
其中,![Rendered by QuickLaTeX.com \[ Av = \lambda v, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-869ca55a56ff575a3d62530e44bdbf4c_l3.png)
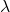 称为特征值,
称为特征值, 称为特征向量
称为特征向量 - 每个特征值满足特征多项式
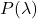 的方程,
的方程,
由代数基本定理,我们可以找到![Rendered by QuickLaTeX.com \[ P(\lambda) = \det(\lambda I - A) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-da65d977f62e5e5eaab77d2f3326c4cc_l3.png)
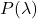 的所有零点(对于一般的域不成立),
的所有零点(对于一般的域不成立),
如果所有零点互不相同,那么我们取![Rendered by QuickLaTeX.com \[ P(\lambda) = (\lambda - \lambda_1) \cdots (\lambda - \lambda_n). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c84a9bd6489555d08c67073a737df98f_l3.png)
 个特征向量
个特征向量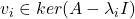 ,即可解决对角化问题。因此,难点在于零点重复的情形,
,即可解决对角化问题。因此,难点在于零点重复的情形,
如果我们取![Rendered by QuickLaTeX.com \[ P(\lambda) = \prod_i (\lambda - \lambda_i)^{n_i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b8f3c4aafe0501bb03ca22f3c4f83650_l3.png)
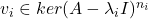 ,那么我们需要证明,这样可以得到
,那么我们需要证明,这样可以得到 个线性无关的向量,即
个线性无关的向量,即![Rendered by QuickLaTeX.com \[ \mathbb{C}^n = \bigoplus_i ker(A - \lambda_iI)^{n_i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8696f15db9fb726a5b2bce6949ba91fc_l3.png)
- (Bézout定理)尽管矩阵的集合是非交换环,然而矩阵
 生成的多项式的集合是交换环,它类似于一元多项式环。对于
生成的多项式的集合是交换环,它类似于一元多项式环。对于
由Bézout定理,存在矩阵![Rendered by QuickLaTeX.com \[ v \in ker(A - \lambda_iI)^{n_i} \cap \sum_{j \neq i} ker(A - \lambda_jI)^{n_j}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-af91dd81c0fa31f047e4c3961dcafd1e_l3.png)
 的多项式
的多项式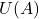 、
、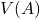 ,满足
,满足
故![Rendered by QuickLaTeX.com \[ U(A)(A - \lambda_iI)^{n_i} + V(A)\prod_{j \neq i} (A - \lambda_jI)^{n_j} = I, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5c3a941c6a1f2ed8ea00d053d9dc8390_l3.png)
从而,![Rendered by QuickLaTeX.com \[ 0 = U(A)(A - \lambda_iI)^{n_i}v + V(A)\prod_{j \neq i} (A - \lambda_jI)^{n_j}v = Iv = v. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a693901140d42da91fbd21e7c5b4d03c_l3.png)
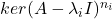 可以构成直和,并且
可以构成直和,并且![Rendered by QuickLaTeX.com \[ \sum_i dimker(A - \lambda_iI)^{n_i} \leq n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ddd5fea02d9eb9a6aa0eec70fd56d887_l3.png)
- (Cayley-Hamilton定理)另一方面,由矩阵乘积的核的不等式,
由下面的Cayley-Hamilton定理,![Rendered by QuickLaTeX.com \[ \sum_i dimker(A - \lambda_iI)^{n_i} \geq dimker\prod_i (A - \lambda_iI)^{n_i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5361da08c56a0fcc43855f37689ee9fa_l3.png)
因此,直和分解成立![Rendered by QuickLaTeX.com \[ dimker\prod_i (A - \lambda_iI)^{n_i} = dimkerP(A) = dimker0 = n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c880b2224cd0a109ee461813319e1fd4_l3.png)
- (Jordan标准型)对任意
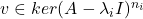 ,如果
,如果 为满足
为满足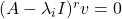 的最小值,那么如下向量组为线性无关的,
的最小值,那么如下向量组为线性无关的,
原因是若![Rendered by QuickLaTeX.com \[ v,\; (A - \lambda_iI)v,\; \ldots,\; (A - \lambda_iI)^{r - 1}v, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e2b5df97111a91de2ece0ff2403f26cc_l3.png)
则![Rendered by QuickLaTeX.com \[ \mu_0v + \mu_1(A - \lambda_iI)v + \cdots + \mu_{r - 1}(A - \lambda_iI)^{r - 1}v = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b6f9ce16ae0ebfba975eaeba6ca174b7_l3.png)
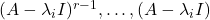 作用于上式,可得
作用于上式,可得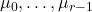 为0。如果取上述形式的向量组作为基底,那么矩阵
为0。如果取上述形式的向量组作为基底,那么矩阵 可以对角化为如下形式的矩阵块,
可以对角化为如下形式的矩阵块,
这称为Jordan标准型,故对于零点重复的情形,矩阵![Rendered by QuickLaTeX.com \[ \begin{bmatrix}\lambda_i\end{bmatrix},\; \begin{bmatrix}\lambda_i & 1 \\ 0 & \lambda_i\end{bmatrix},\; \begin{bmatrix}\lambda_i & 1 & 0 \\ 0 & \lambda_i & 1 \\ 0 & 0 & \lambda_i\end{bmatrix},\; \ldots \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4316ce8155b5c5ee04fc5f9a98daeb90_l3.png)
 不一定能完全对角化
不一定能完全对角化
- (Bézout定理)尽管矩阵的集合是非交换环,然而矩阵
- Cayley-Hamilton定理是指
受到知乎的启发,我们可以用复分析的方法来证明(对于一般的域,我们可以用代数方法来证明)![Rendered by QuickLaTeX.com \[ P(A) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-119bd3bb5fec6ec64957b09a1f624dbd_l3.png)
- 由于
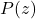 为多项式,故它为
为多项式,故它为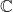 上的全纯函数。由Cauchy积分公式,
上的全纯函数。由Cauchy积分公式,
将![Rendered by QuickLaTeX.com \[ P(w) = \frac{1}{2\pi i}\int_{\partial\Omega} \frac{P(z)}{z - w}dz. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-64de85b7e4e10e4e12dd7f2f697baea7_l3.png)
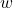 转换为矩阵
转换为矩阵 ,
,![Rendered by QuickLaTeX.com \[ P(A) = \frac{1}{2\pi i}\int_{\partial\Omega} P(z)(zI - A)^{-1}dz. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-208b5c7061cba0effc96182855c55cb5_l3.png)
- 注意,
并且伴随矩阵的系数全部为行列式(即多项式),故它们为![Rendered by QuickLaTeX.com \[ P(z)(zI - A)^{-1} = \det(zI - A)(zI - A)^{-1} = adj(zI - A), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cece0ffef473aebe8371b14227b31b2c_l3.png)
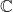 上的全纯函数。由Cauchy积分定理,
上的全纯函数。由Cauchy积分定理,![Rendered by QuickLaTeX.com \[ P(A) = \frac{1}{2\pi i}\int_{\partial\Omega} adj(zI - A)dz = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c85e086ea14c0069a7ffdde3e2c9fa06_l3.png)
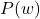 为有奇点的情形,但是利用伴随矩阵、行列式的性质,
为有奇点的情形,但是利用伴随矩阵、行列式的性质,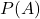 为没有奇点的情形,所以Cayley-Hamilton定理成立
为没有奇点的情形,所以Cayley-Hamilton定理成立
- 由于
从QR分解到奇异值分解
- 为了从直和分解进入正交分解,我们需要将基底转换为单位正交基
 上的内积、范数分别为
上的内积、范数分别为
如果一个向量的范数为1,那么它称为单位向量。如果两个向量的内积为0,那么它们称为正交的。因此,单位正交基等价于![Rendered by QuickLaTeX.com \[ \langle{x, y}\rangle_{\mathbb{C}^n} = x^T\overline{y},\; ||x|| = \sqrt{\langle{x, x}\rangle_{\mathbb{C}^n}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6c0bf72e8886fed55f628ef9cf5795d1_l3.png)
注意,正交强于线性无关![Rendered by QuickLaTeX.com \[ \langle{e_i, e_j}\rangle_{\mathbb{C}^n} = \delta_{ij},\; 1 \leq i, j \leq n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c621c666aa35aa4b3e83aa8042ed81f2_l3.png)
- 伴随算子
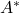 为转置共轭,
为转置共轭,
Hermite矩阵满足![Rendered by QuickLaTeX.com \[ \langle{Ax, y}\rangle_{\mathbb{C}^n} = (Ax)^T\overline{y} = x^T\overline{\overline{A^T}y} = \langle{x, A^*y}\rangle_{\mathbb{C}^n}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3427da72a8d129721c8b21049803a593_l3.png)
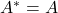 ,酉矩阵满足
,酉矩阵满足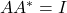 (在实数域上,如果内积中的
(在实数域上,如果内积中的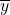 更换为
更换为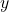 、Hermite矩阵更换为实对称矩阵
、Hermite矩阵更换为实对称矩阵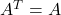 、酉矩阵更换为正交矩阵
、酉矩阵更换为正交矩阵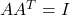 ,那么我们可以得到下面的所有结果)
,那么我们可以得到下面的所有结果)
- (Gram-Schmidt正交化)设一组基底为
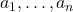 。我们将
。我们将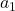 单位化得到
单位化得到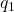 ,将
,将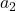 减去
减去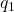 常数倍并单位化得到
常数倍并单位化得到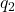 ,重复这一过程,直到得到单位正交基
,重复这一过程,直到得到单位正交基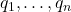
- function
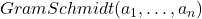
- for
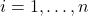
- for

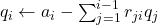
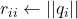
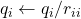
- for
- return

- for
- function
- (QR分解)如果将
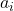 作为可逆矩阵
作为可逆矩阵 、将
、将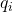 作为酉矩阵
作为酉矩阵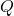 、将
、将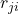 作为上三角矩阵
作为上三角矩阵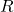 ,那么我们可以得到QR分解
,那么我们可以得到QR分解
同时,利用Gram-Schmidt正交化,我们可以找到一组单位正交基,或者将单位正交的向量组扩充为一组单位正交基![Rendered by QuickLaTeX.com \[ A = QR. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e539fc30b6bbbe8e5647e94917706778_l3.png)
- (Hermite矩阵的特征值)如果
 为Hermite矩阵,那么直和分解具有更好的性质
为Hermite矩阵,那么直和分解具有更好的性质![Rendered by QuickLaTeX.com \[ \mathbb{C}^n = \bigoplus_i ker(A - \lambda_iI)^{n_i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8696f15db9fb726a5b2bce6949ba91fc_l3.png)
- 对于特征值
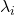 、特征向量
、特征向量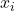 ,利用伴随算子的性质,
,利用伴随算子的性质,
因此,![Rendered by QuickLaTeX.com \[ \lambda_i||x_i||^2 = \langle{Ax_i, x_i}\rangle_{\mathbb{C}^n} = \langle{x_i, Ax_i}\rangle_{\mathbb{C}^n} = \overline{\lambda_i}||x_i||^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2dd6700276994ad0b6e6be5f2808b7ca_l3.png)
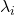 为实数(在实数域上,特征值、特征值的共轭是成对出现的,所以我们可以将它们更换为2个实特征值)
为实数(在实数域上,特征值、特征值的共轭是成对出现的,所以我们可以将它们更换为2个实特征值) - 对于
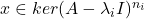 ,利用伴随算子的性质,
,利用伴随算子的性质,
因此,![Rendered by QuickLaTeX.com \[ 0 = \langle{(A - \lambda_iI)^{n_i}x, (A - \lambda_iI)^{n_i - 2}x}\rangle_{\mathbb{C}^n} = ||(A - \lambda_iI)^{n_i - 1}x||^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f2a84253ec76b7b1a05d46e33ae177b1_l3.png)
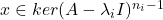 。重复这一过程,直到得到
。重复这一过程,直到得到![Rendered by QuickLaTeX.com \[ ker(A - \lambda_iI)^{n_i} = ker(A - \lambda_iI). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-10b6d5abc293fe56e50c2a92af89031d_l3.png)
- 对于
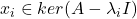 、
、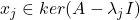 ,利用伴随算子的性质,
,利用伴随算子的性质,
因此,![Rendered by QuickLaTeX.com \[ \lambda_i\langle{x_i, x_j}\rangle_{\mathbb{C}^n} = \langle{Ax_i, x_j}\rangle_{\mathbb{C}^n} = \langle{x_i, Ax_j}\rangle_{\mathbb{C}^n} = \lambda_j\langle{x_i, x_j}\rangle_{\mathbb{C}^n}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cf6c8cdca5932fbf40559f2abb38c45d_l3.png)
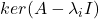 、
、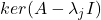 正交
正交 - 最终,我们可以得到正交分解
进一步,在每个![Rendered by QuickLaTeX.com \[ \mathbb{C}^n = \bigoplus_i ker(A - \lambda_iI). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-aef260e2dd73c8ae925376fd6c549770_l3.png)
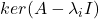 中取一组单位正交基。如果将单位正交基作为酉矩阵
中取一组单位正交基。如果将单位正交基作为酉矩阵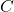 、将特征值
、将特征值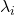 作为对角矩阵
作为对角矩阵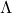 ,那么矩阵
,那么矩阵 可以完全对角化
可以完全对角化![Rendered by QuickLaTeX.com \[ C^*AC = C^{-1}AC = \Lambda. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ac683a5472477c9de7dc02285680de34_l3.png)
- 对于特征值
- (奇异值分解)到现在为止,我们只考虑了
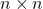 的矩阵
的矩阵 。在数值计算中,我们需要考虑
。在数值计算中,我们需要考虑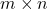 的矩阵
的矩阵 ,此时特征值推广为奇异值
,此时特征值推广为奇异值
- 注意,
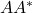 为
为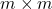 的Hermite矩阵,故存在
的Hermite矩阵,故存在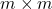 的酉矩阵
的酉矩阵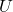 ,使得
,使得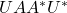 为对角矩阵。令
为对角矩阵。令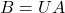 ,类似于半正定矩阵,我们有
,类似于半正定矩阵,我们有
因此,对角矩阵的元素非负,我们取一个对角元素为正的对角矩阵块![Rendered by QuickLaTeX.com \[ x^TBB^*\overline{x} = ||B^Tx||^2 \geq 0,\; x \in \mathbb{C}^m. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b31f90d10603bedf844f3098356e7d00_l3.png)
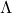 ,然后对矩阵
,然后对矩阵 进行分块,
进行分块,![Rendered by QuickLaTeX.com \[ BB^* = \begin{bmatrix}\Lambda^2 & 0 \\ 0 & 0\end{bmatrix},\; \begin{bmatrix}B_1 \\ B_2\end{bmatrix}\begin{bmatrix}B_1^* & B_2^*\end{bmatrix} = \begin{bmatrix}\Lambda^2 & 0 \\ 0 & 0\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1118a6b724d6d11a98a9690529b65d7f_l3.png)
- 对于矩阵
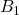 、
、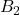 ,我们有
,我们有
由第二式的对角线,可得![Rendered by QuickLaTeX.com \[ B_1B_1^* = \Lambda^2,\; B_2B_2^* = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1972cd98c46fff81aab08582d34d1833_l3.png)
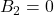 。由第一式,可得
。由第一式,可得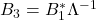 的列向量构成单位正交的向量组,
的列向量构成单位正交的向量组,
将其扩充为一组单位正交基,可得![Rendered by QuickLaTeX.com \[ B_3^*B_3 = \Lambda^{-1}B_1B_1^*\Lambda^{-1} = I. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dc12c2ffe6f53b3aff8df5ead226a66b_l3.png)
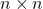 的酉矩阵
的酉矩阵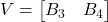 。最终,我们可以得到奇异值分解,
。最终,我们可以得到奇异值分解,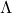 的对角元素为矩阵
的对角元素为矩阵 的奇异值,
的奇异值,![Rendered by QuickLaTeX.com \[ UAV = BV = \begin{bmatrix}B_1 \\ 0\end{bmatrix}\begin{bmatrix}B_3 & B_4\end{bmatrix} = \begin{bmatrix}\Lambda & 0 \\ 0 & 0\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e703fc135f90ff60b91398a4ac2bbf61_l3.png)
- 注意,