参考资料:Graph Theory An Introductory Course
图
- 图
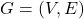
- 顶点的集合
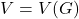 ,它对应于图的阶
,它对应于图的阶![Rendered by QuickLaTeX.com \[ order(G) = card(V(G)). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9820307db8c7af156d801ac1c9f00d72_l3.png)
- 边的集合
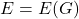 ,它对应于图的大小
,它对应于图的大小![Rendered by QuickLaTeX.com \[ size(G) = card(E(G)). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b34197b0e31d0fd6b97cd027b3e922b8_l3.png)
- 如果阶为
 ,那么大小为
,那么大小为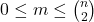
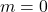 ,对应于空图
,对应于空图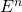
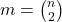 ,对应于完全图
,对应于完全图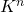
- 顶点的集合
- 图的范畴
- 子图
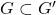
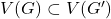 ,
,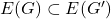
- 同态
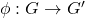
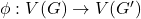 ,
,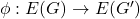
- 子图
- 顶点度数(Degree)
- 设
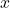 的相邻顶点集为
的相邻顶点集为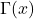 。那么,顶点度数为
。那么,顶点度数为
最小、最大的顶点度数分别记为![Rendered by QuickLaTeX.com \[ d(x) = card(\Gamma(x)). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-44e58fc307cd7d0c021132f988fd602b_l3.png)
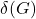 、
、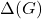
- 握手引理
故![Rendered by QuickLaTeX.com \[ \sum_{i = 1}^n d(x_i) = 2e(G), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e223fa46550bcea6938fba4f9901cfe_l3.png)
如果![Rendered by QuickLaTeX.com \[ \delta(G) \leq \frac{2e(G)}{n} \leq \Delta(G). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-58251829acac4414faf7dbf1d7873466_l3.png)
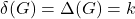 ,那么
,那么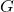 称为
称为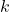 -正则图
-正则图
- 设
- 将
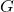 视为一个1维单纯复形
视为一个1维单纯复形
- 道路(Path)为(起点、终点为顶点的)连续映射
![Rendered by QuickLaTeX.com [0, 1] \to |G|](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f7c2bdf6fab417e35795ae6252f42e7b_l3.png)
- 闭道路(Closed Path)为(基点为顶点的)连续映射
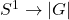
- 环路(Cycle)为(基点为顶点的)嵌入
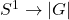
- 如果
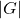 可以嵌入
可以嵌入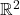 ,那么
,那么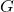 称为平面图
称为平面图 - 如果
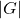 连通(等价于道路连通),那么
连通(等价于道路连通),那么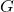 称为连通图
称为连通图
- 道路(Path)为(起点、终点为顶点的)连续映射
- 无环路的图称为森林(Forest),无环路的连通图称为树(Tree)
- 森林即
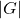 的1维同调群为0,树即
的1维同调群为0,树即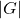 的1维同调群为0、0维同调群为
的1维同调群为0、0维同调群为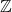
- 森林即
图上的空间
- 利用边缘算子,我们可以得到闭链群