随机过程
- 噪声是一种随机信号,随机信号可以表示为随机过程
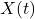
- 对于随机过程,我们可以取某些量的数学期望,然后进行分析
- 均值、方差
![Rendered by QuickLaTeX.com \[ \mu(t) = \mathbb{E}[X(t)],\; \sigma^2(t) = \mathbb{E}[|X(t)|^2] - \mu(t)^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9b01d642917a6cfa921c4c4beaeeacd9_l3.png)
- 协方差、自相关函数
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} Cov(t_1, t_2) &= \mathbb{E}[X(t_1)X(t_2)] - \mu(t_1)\mu(t_2), \\ R(t_1, t_2) &= \mathbb{E}[X(t_1)X(t_2)]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-10b4711e5ba902668da4bdc09c516a29_l3.png)
- 均值、方差
- 由定义可知,从均值、自相关函数可以得到方差、协方差。如果
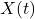 的均值、自相关函数在时间平移下不变,即
的均值、自相关函数在时间平移下不变,即
那么,![Rendered by QuickLaTeX.com \[ \mu(t) = \mu(0) = const,\; R(t, t + \tau) = R(0, \tau) = R(\tau), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c11cf643e66f2c851555c3907b2f862f_l3.png)
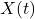 称为平稳过程。此时
称为平稳过程。此时
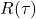 为偶函数
为偶函数![Rendered by QuickLaTeX.com \[ R(-\tau) = \mathbb{E}[X(t)X(t - \tau)] = \mathbb{E}[X(t + \tau)X(t)] = R(\tau). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c9311c67ec3b8c738aaf391794c56ccc_l3.png)
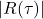 在
在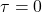 处达到最大值
处达到最大值![Rendered by QuickLaTeX.com \[ |R(\tau)| \leq \frac 12\bigg\{\mathbb{E}[|X(t)|^2] + \mathbb{E}[|X(t + \tau)|^2]\bigg\} = R(0). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ca096e3abc0686b49761db9c29cb73b5_l3.png)
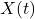 在时间
在时间![Rendered by QuickLaTeX.com [0, T]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-19c12377c4f37daa529dbd63f3f2c26c_l3.png) 上的平均功率为
上的平均功率为![Rendered by QuickLaTeX.com \[ P = \mathbb{E}\bigg[\frac 1T\int_0^T |X(t)|^2dt\bigg] = \frac 1T\int_0^T \mathbb{E}[|X(t)|^2]dt = R(0). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-03c15d3f9004a44150179b3d90a2c066_l3.png)
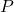 也可以在频域上计算,我们使用频率响应和采样率中的Fourier变换。令
也可以在频域上计算,我们使用频率响应和采样率中的Fourier变换。令![Rendered by QuickLaTeX.com X_T(t) = X(t)1_{[0, T]}(t)](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f706ec35ea3060b8603bcf8367cb6b89_l3.png) ,由Plancherel定理,考虑如下的数学期望
,由Plancherel定理,考虑如下的数学期望
其中,![Rendered by QuickLaTeX.com \[ \mathbb{E}\bigg[\frac 1T\frac{1}{2\pi}\int_{-\infty}^{+\infty} |\widehat{X_T}(\omega)|^2d\omega\bigg] = \frac{1}{2\pi}\int_{-\infty}^{+\infty} \mathbb{E}\bigg[\frac 1T|\widehat{X_T}(\omega)|^2\bigg]d\omega, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9e6a5a3e31f9b859fbffd0a46bcc39f7_l3.png)
如果![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \mathbb{E}\bigg[\frac 1T|\widehat{X_T}(\omega)|^2\bigg] &= \mathbb{E}\bigg[\frac 1T\int_0^TX(t)e^{-j\omega t}dt\int_0^TX(s)e^{j\omega s}ds\bigg] \\ &= \frac 1T\int_0^T\int_0^T \mathbb{E}[X(t)X(s)]e^{-j\omega(t - s)}dtds. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-addd4cf386923c4bcf3053ee015b7423_l3.png)
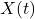 为平稳过程,那么
为平稳过程,那么![Rendered by QuickLaTeX.com \mathbb{E}[X(t)X(s)] = R(t - s)](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a27f4b2670fb953954cfadd411c24605_l3.png)
- 接下来计算积分。令
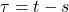 ,由Fubini定理,
,由Fubini定理,
由Lebesgue控制收敛定理,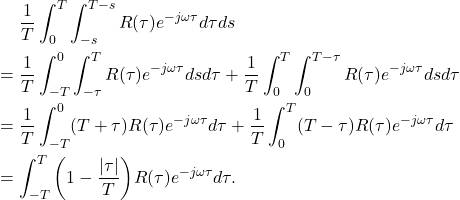
![Rendered by QuickLaTeX.com \[ \lim_{T \to +\infty} \int_{-\infty}^{+\infty} \bigg(1 - \frac{|\tau|}{T}\bigg)1_{[-T, T]}R(\tau)e^{-j\omega\tau}d\tau = \int_{-\infty}^{+\infty} R(\tau)e^{-j\omega\tau}d\tau. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-26009c370223fe44df8aeeea958be05d_l3.png)
- 因此,我们有如下的Wiener–Khinchin定理
同时,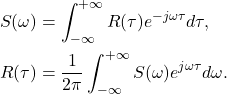
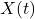 在时间
在时间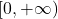 上的平均功率可以同时在时域和频域上计算,
上的平均功率可以同时在时域和频域上计算,
因为![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} P &= \lim_{T \to +\infty}\int_{-\infty}^{+\infty} \mathbb{E}\bigg[\frac 1T|X_T(t)|^2\bigg]dt = R(0), \\ P &= \lim_{T \to +\infty}\frac{1}{2\pi}\int_{-\infty}^{+\infty} \mathbb{E}\bigg[\frac 1T|\widehat{X_T}(\omega)|^2\bigg]d\omega = \frac{1}{2\pi}\int_{-\infty}^{+\infty} S(\omega)d\omega. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4bd7751f0afa287b97a037dd360a84b8_l3.png)
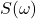 对应于平均功率
对应于平均功率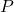 在频域
在频域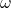 上的密度函数,所以它称为功率谱密度(Power Spectral Density,PSD)
上的密度函数,所以它称为功率谱密度(Power Spectral Density,PSD)
Gauss变量、Gauss向量和Gauss过程
- Gauss变量
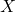
- 概率密度函数为
![Rendered by QuickLaTeX.com \[ p_X(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x - \mu)^2}{2\sigma^2}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-174b0274e6e34964a93dd10b9f95cf8e_l3.png)
- 均值、方差分别为
![Rendered by QuickLaTeX.com \[ \mathbb{E}[X] = \int_{-\infty}^{+\infty} (x - \mu)p_X(x)dx + \int_{-\infty}^{+\infty} \mu p_X(x)dx = 0 + \mu = \mu, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c20e8750341c57425540cf6b50e208e0_l3.png)
也就是说,Gauss变量可以由均值、方差完全确定。此时,我们也称![Rendered by QuickLaTeX.com \[ Var(X) = \int_{-\infty}^{+\infty} (x - \mu)^2p_X(x)dx = \frac{2\sigma^2}{\sqrt{\pi}}\Gamma\bigg(\frac 32\bigg) = \sigma^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fc5329bf39233480458d19b910aec06c_l3.png)
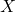 满足正态分布
满足正态分布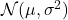 ,记为
,记为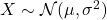
- 类似于Fourier变换和中心极限定理,计算
因此,对任意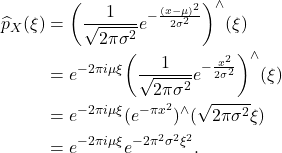
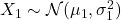 ,
, 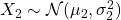 ,我们有
,我们有
从而,![Rendered by QuickLaTeX.com \[ \widehat{p}_{X_1 + X_2}(\xi) = \widehat{p}_{X_1}(\xi)\widehat{p}_{X_2}(\xi) = e^{-2\pi i(\mu_1 + \mu_2)\xi}e^{-2\pi^2(\sigma_1^2 + \sigma_2^2)\xi^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c4584122d3a8a238bfb571daa967cb8e_l3.png)
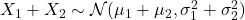 。一般地,Gauss变量的线性组合仍然是Gauss变量
。一般地,Gauss变量的线性组合仍然是Gauss变量
- 概率密度函数为
- Gauss向量
 ,其中
,其中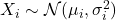
- 首先考虑最简单的情形,即
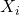 相互独立。此时,
相互独立。此时,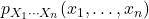 为
为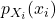 的乘积,
的乘积,
令![Rendered by QuickLaTeX.com \[ \frac{1}{(2\pi)^{\frac n2}\prod_{i = 1}^n \sigma_i}\exp\bigg[-\frac 12\sum_{i = 1}^n \frac{(x_i - \mu_i)^2}{\sigma_i^2}\bigg]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1fe636f56235e48de0399f02baeecfd9_l3.png)
那么,![Rendered by QuickLaTeX.com \[ \mu = \begin{bmatrix}\mu_1 \\ \vdots \\ \mu_n\end{bmatrix},\; \Sigma = \begin{bmatrix}\sigma_1^2 & & \\ & \ddots & \\ & & \sigma_n^2\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-200194c476bb68d152f2efa277cf7629_l3.png)
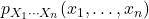 等于
等于![Rendered by QuickLaTeX.com \[ \frac{1}{(2\pi)^{\frac n2}(\det\Sigma)^{\frac 12}}\exp\bigg[-\frac 12(x - \mu)^T\Sigma^{-1}(x - \mu)\bigg]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-05dd331e0c2b7544d1700200d0a9c965_l3.png)
- 其次考虑一般情形,即
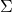 为实对称的、正定的矩阵。由数值线性代数可知,存在
为实对称的、正定的矩阵。由数值线性代数可知,存在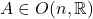 ,使得
,使得
我们也有![Rendered by QuickLaTeX.com \[ A^{-1}\Sigma A = A^T\Sigma A = \begin{bmatrix}\sigma_1^2 & & \\ & \ddots & \\ & & \sigma_n^2\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8df0f0816a5ecd28c8aa9713e3a3517d_l3.png)
![Rendered by QuickLaTeX.com \[ A^{-1}\Sigma^{-1}A = A^T\Sigma^{-1}A = \begin{bmatrix}\sigma_1^{-2} & & \\ & \ddots & \\ & & \sigma_n^{-2}\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-75931750338478a73602d987bd7b1352_l3.png)
- 令
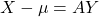 。那么,
。那么,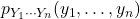 等于
等于
由此可知,![Rendered by QuickLaTeX.com \[ \frac{1}{(2\pi)^{\frac n2}\prod_{i = 1}^n \sigma_i}\exp\bigg(-\frac 12\sum_{i = 1}^n \frac{y_i^2}{\sigma_i^2}\bigg). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-57405bb928c31981bbeddd7dcc8e5288_l3.png)
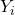 相互独立,并且
相互独立,并且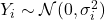 。从而,
。从而,
因此,如果![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \mathbb{E}[X] &= \mu + A\mathbb{E}[Y] = \mu, \\ Cov(X_i, X_j) &= \mathbb{E}\bigg[\bigg(\sum_{p = 1}^n A_{ip}Y_p\bigg) \cdot \bigg(\sum_{q = 1}^n A_{jq}Y_q\bigg)\bigg] \\ &= \sum_{p, q = 1}^n A_{ip}A_{jq}\mathbb{E}[Y_pY_q] \\ &= \sum_{p = 1}^n A_{ip}A_{jp}\sigma_p^2 = \Sigma_{ij}. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5f8f3ec7b65514de04f50fafffc1844f_l3.png)
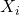 、
、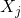 不相关(
不相关(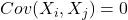 ),那么二者独立(
),那么二者独立(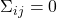 )
)
- 首先考虑最简单的情形,即
- Gauss过程
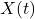
- 如果任意时间序列
 为Gauss向量,那么
为Gauss向量,那么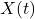 称为Gauss过程
称为Gauss过程 - 由上面的笔记可知,任意时间序列的联合概率密度函数可以由均值
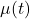 、协方差
、协方差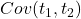 完全确定。我们通常考虑均值为0的、平稳的Gauss过程,所以我们只需确定自相关函数
完全确定。我们通常考虑均值为0的、平稳的Gauss过程,所以我们只需确定自相关函数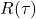 即可
即可
- 如果任意时间序列
噪声的类型
- 白噪声(White Noise,WN)
- 我们有
白噪声的平均功率为![Rendered by QuickLaTeX.com \[ S_{wn}(\omega) = A,\; R_{wn}(\tau) = A\delta(\tau). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5a20a6ed30d11da73dab81409d9ef0e6_l3.png)
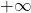 ,所以它是一个理想模型,实际上无法实现
,所以它是一个理想模型,实际上无法实现
- 我们有
- 带宽有限的白噪声(Band-limited White Noise,BWN)
- 我们有
带宽有限的白噪声的平均功率为![Rendered by QuickLaTeX.com \[ S_{bwn}(\omega) = A1_{[-2\pi W, 2\pi W]},\; R_{bwn}(\tau) = 2WA\frac{\sin(2\pi W\tau)}{2\pi W\tau}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b1901fd7ffca5c68803af3f213a790eb_l3.png)
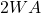 ,所以它可以实现
,所以它可以实现 - 根据频率响应和采样率,如果我们用Nyquist采样率
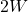 来采样,那么时间间隔
来采样,那么时间间隔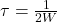 ,噪声恰好是不相关的
,噪声恰好是不相关的
- 我们有
- Gauss白噪声(White Gaussian Noise,WGN)
- 在Gauss过程中,取
Gauss白噪声是一种白噪声,实际上无法实现;事实上,它无法用概率密度函数来描述。不过,Gauss白噪声可以用于构造Brown运动![Rendered by QuickLaTeX.com \[ R_{wgn}(\tau) = A\delta(\tau). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-99b910eb285017a25c57d515cdc04ad8_l3.png)
- 在实际的通信中,我们考虑加性Gauss白噪声(Additive White Gaussian Noise,AWGN),取
加性Gauss白噪声的平均功率为![Rendered by QuickLaTeX.com \[ R_{awgn}(\tau) = 0,\; \tau \neq 0;\; R_{awgn}(0) = \sigma^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dbb14ab30e2c3d9c50b903c128666334_l3.png)
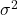 。同时,我们有
。同时,我们有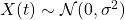 ,并且不同时刻的
,并且不同时刻的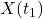 、
、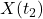 是独立的
是独立的
- 在Gauss过程中,取