硅晶体
- 硅晶体的基本结构是单位晶胞(Unit Cell)
- 每个单位晶胞都是一个正方体,正方体的边长称为晶格常数(Lattice Constant),硅晶体的晶格常数为5.43Å
- 有8个原子位于顶点,有6个原子位于面的中心
- 如果我们将单位晶胞等分为8个小正方体,那么有4个原子位于小正方体的中心——2个原子在上面(左后、右前),2个原子在下面(左前、右后)
- 通过平移,单位晶胞可以填满3维空间,并且每个原子都与最近的4个原子形成4个键
- 一个键包含两个共价的电子。在绝对零度下,电子无法挣脱键的束缚;在其他温度下,热能会使一些电子挣脱键的束缚,成为自由电子(带负电),原来的地方留下空穴(带正电)
- 在室温下,电子和空穴的浓度通常很低。如果需要引入更多的电子和空穴,那么可以进行掺杂(Doping),即掺入杂质原子
- N型:加入施主(Donor),通常为V族原子,它们可以施舍电子
- N+型:施主浓度很高
- P型:加入受主(Acceptor),通常为III族原子,它们可以接受电子
- P+型:受主浓度很高
- 原子中的电子的特点
- 在一个原子中,每个电子占据一个能级(Energy Level)
- 在
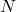 个接近的原子中,由Pauli不相容原理,每个能级分裂为
个接近的原子中,由Pauli不相容原理,每个能级分裂为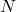 个
个 - 在硅晶体中,
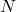 通常很大。因此,分裂出来的能级很密集,会形成近似连续的能带(Energy Band)
通常很大。因此,分裂出来的能级很密集,会形成近似连续的能带(Energy Band)
- 电子倾向于从低到高占据能带。几乎填满电子的最高一条能带称为价带(Valence Band),几乎没有电子的最低一条能带称为导带(Conduction Band),二者之间为能带间隙(Band Gap)
- 设
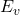 为价带顶,
为价带顶,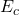 为导带底。那么,能带间隙的宽度为
为导带底。那么,能带间隙的宽度为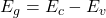
- 绝缘体的
 较大,半导体的
较大,半导体的 较小,导体的
较小,导体的 为0。其中,硅是常用的半导体
为0。其中,硅是常用的半导体
- 设
状态密度
- 设
 为硅晶体中的正方体的边长。对于
为硅晶体中的正方体的边长。对于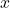 方向(
方向(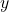 ,
, 方向是类似的),波长只能是
方向是类似的),波长只能是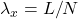 ,动量只能是
,动量只能是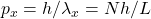 ,其中
,其中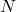 为正整数。因此,在动量空间中,平均每2个状态(考虑到2个自旋方向)对应的体积为
为正整数。因此,在动量空间中,平均每2个状态(考虑到2个自旋方向)对应的体积为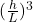
- 现在,我们将动量转化为能量
- 由
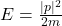 可知,
可知,![Rendered by QuickLaTeX.com \[ \frac{dE}{d|p|} = \frac {|p|}{m} = \sqrt{\frac{2E}{m}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-93402030cd9fae65ba11b36854820655_l3.png)
- 在能量为
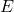 时,动量空间的体积为
时,动量空间的体积为![Rendered by QuickLaTeX.com \[ 4\pi|p|^2d|p| = 8\pi mE \cdot \sqrt{\frac{m}{2E}}dE. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-58ce9aa9cc2e409734386c1e0bc60cb5_l3.png)
- 在该体积中的状态数量为
![Rendered by QuickLaTeX.com \[ 4\pi|p|^2d|p| \times 2 \div \bigg(\frac hL\bigg)^3 = \frac{8\pi m\sqrt{2mE}L^3}{h^3}dE \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cfe2f527aa9707f8278e1a1ea6044c9b_l3.png)
- 由
- 导带和价带的状态密度(Density of States)
- 导带:质量为电子的有效质量
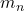 ,能量为
,能量为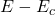 ,故状态密度为
,故状态密度为![Rendered by QuickLaTeX.com \[ D_c(E) = \frac{8\pi m_n\sqrt{2m_n(E - E_c)}}{h^3}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4b78ab5a1f81a30aa56aa504b71b3f29_l3.png)
- 价带:质量为空穴的有效质量
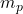 ,能量为
,能量为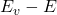 ,故状态密度为
,故状态密度为![Rendered by QuickLaTeX.com \[ D_v(E) = \frac{8\pi m_p\sqrt{2m_p(E_v - E)}}{h^3}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-30747d8921a1408a052ad919b25cf2a5_l3.png)
- 导带:质量为电子的有效质量
Fermi函数
- 设
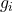 为能量
为能量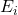 的状态数量,
的状态数量,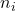 为能量
为能量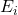 的电子数量,
的电子数量,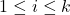 。将电子分配到状态中的方法数为
。将电子分配到状态中的方法数为
由Stirling估计,![Rendered by QuickLaTeX.com \[ W = \prod_i \frac{g_i!}{(g_i - n_i)!n_i!}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cf17b33cb59ebb6b49cb51c51a7f684b_l3.png)
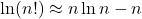 ,故
,故![Rendered by QuickLaTeX.com \[ \ln W \approx g_i\ln g_i - (g_i - n_i)\ln(g_i - n_i) - n_i\ln n_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4dc78f3c2308950bea298edec43eaa2d_l3.png)
- 在平衡状态(Equilibrium)下,
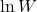 在如下约束下达到极大值
在如下约束下达到极大值
其中![Rendered by QuickLaTeX.com \[ \sum_i n_i = N,\; \sum_i n_iE_i = E, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c0553051c473053eb0805d1bd68f5c55_l3.png)
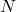 为总电子数,
为总电子数,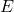 为总能量。以下求解条件极值问题
为总能量。以下求解条件极值问题
- 由Lagrange乘子法,令
![Rendered by QuickLaTeX.com \[ \varphi(n_i, \lambda, \mu) = \ln W + \lambda\bigg(N - \sum_i n_i\bigg) + \mu\bigg(E - \sum_i n_iE_i\bigg). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-16acbb7535d3c3004779d99c5ccf3ecc_l3.png)
- 在
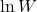 的极值点处,
的极值点处,
因此,![Rendered by QuickLaTeX.com \[ 0 = \frac{\partial \varphi}{\partial n_i} = \ln(g_i - n_i) - \ln n_i - \lambda - \mu E_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c3fb277275849dd061a4eb92cb244e93_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{g_i - n_i}{n_i} = e^{\lambda + \mu E_i},\; \frac{n_i}{g_i} = \frac{1}{1 + e^{\lambda + \mu E_i}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a62895b6be5a2eb668dcfb8475fb0969_l3.png)
- 由Lagrange乘子法,令
- Fermi函数(Fermi Function)的形式为
并且![Rendered by QuickLaTeX.com \[ f(E) = \frac{1}{1 + e^{\lambda + \mu E}}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b60089e8b01f47f75882c0d58001dbf2_l3.png)
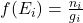 表示电子占据能量
表示电子占据能量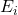 的概率
的概率
- 平均能量可以通过下式计算
我们使用近似![Rendered by QuickLaTeX.com \[ \frac{\int_{E_c}^{+\infty} (E - E_c) \cdot D_c(E) \cdot f(E)dE}{\int_{E_c}^{+\infty} D_c(E) \cdot f(E)dE}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-20405432270c3081ff2bddfe723fe967_l3.png)
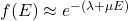 ,积分的结果为
,积分的结果为
另一方面,在温度为![Rendered by QuickLaTeX.com \[ \frac{\mu^{-\frac 52}\Gamma(\frac 52)}{\mu^{-\frac 32}\Gamma(\frac 32)} = \frac 32\mu^{-1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-705ba8eed8847b2da86b919e981c1735_l3.png)
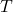 时,平均能量为
时,平均能量为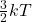 ,故
,故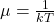
- 最后,令
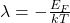 ,其中
,其中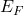 称为Fermi能级(Fermi Level),故
称为Fermi能级(Fermi Level),故![Rendered by QuickLaTeX.com \[ f(E) = \frac{1}{1 + e^{\frac{E - E_F}{kT}}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0af4fa7aa6f61bf6150fe39d1691efb2_l3.png)
- 平均能量可以通过下式计算
电子和空穴的浓度
- 在下面的计算中,我们使用如下近似
- 电子占据能量
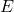 的概率为
的概率为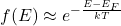
- 空穴占据能量
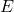 的概率为
的概率为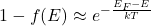
- 电子占据能量
- 电子浓度为
令![Rendered by QuickLaTeX.com \[\begin{split} n &= \int_{E_c}^{+\infty} D_c(E)f(E)dE \\ &= \int_{E_c}^{+\infty} \frac{8\pi m_n\sqrt{2m_n(E - E_c)}}{h^3} \cdot e^{-\frac{E - E_F}{kT}}dE \\ &= \frac{8\pi m_n\sqrt{2m_n}}{h^3} \cdot (kT)^{\frac 32}e^{-\frac{E_c - E_F}{kT}} \cdot \Gamma\bigg(\frac 32\bigg). \\ &= 2\bigg(\frac{2\pi m_nkT}{h^2}\bigg)^{\frac 32}e^{-\frac{E_c - E_F}{kT}}. \end{split}\]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f3eeb0ac262f40ffbb8bc8a6db08dfe1_l3.png)
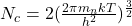 为导带的有效状态密度(Effective Density of States of the Conduction Band)。那么,
为导带的有效状态密度(Effective Density of States of the Conduction Band)。那么,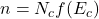 ,这等价于所有电子位于能量
,这等价于所有电子位于能量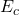 处,且状态密度为
处,且状态密度为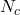
- 空穴浓度为
令![Rendered by QuickLaTeX.com \[\begin{split} p &= \int_{-\infty}^{E_v} D_v(E)[1 - f(E)]dE \\ &= \int_{-\infty}^{E_v} \frac{8\pi m_p\sqrt{2m_p(E_v - E)}}{h^3} \cdot e^{-\frac{E_F - E}{kT}}dE \\ &= \frac{8\pi m_p\sqrt{2m_p}}{h^3} \cdot (kT)^{\frac 32}e^{-\frac{E_F - E_v}{kT}} \cdot \Gamma\bigg(\frac 32\bigg). \\ &= 2\bigg(\frac{2\pi m_pkT}{h^2}\bigg)^{\frac 32}e^{-\frac{E_F - E_v}{kT}}. \end{aligned}\]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-156f3dbade90669543aced7729d6837a_l3.png)
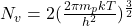 为价带的有效状态密度(Effective Density of States of the Valence Band)。那么,
为价带的有效状态密度(Effective Density of States of the Valence Band)。那么,![Rendered by QuickLaTeX.com p = N_v[1 - f(E_v)]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6e677be05d5142447dff8bf2e78dfdbe_l3.png) ,这等价于所有空穴位于能量
,这等价于所有空穴位于能量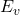 处,且状态密度为
处,且状态密度为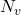
- 掺杂后的电子和空穴的浓度
- 定义本征载流子浓度(Intrinsic Carrier Concentration)
令![Rendered by QuickLaTeX.com \[ n_i^2 = np = N_cN_ve^{-\frac{E_g}{kT}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e61538c465ae4d556fac96ff172f9ca5_l3.png)
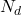 为施主浓度,
为施主浓度,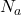 为受主浓度。由于
为受主浓度。由于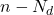 和
和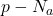 分别为半导体本身贡献的电子和空穴的浓度,故
分别为半导体本身贡献的电子和空穴的浓度,故![Rendered by QuickLaTeX.com \[ n - N_d = p - N_a. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e22df57163aa91f3f02dffb1bf0c290e_l3.png)
- 从而,
![Rendered by QuickLaTeX.com \[ n = \frac{N_d - N_a}{2} + \sqrt{\bigg(\frac{N_d - N_a}{2}\bigg)^2 + n_i^2}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b013060a1539938a47acf986df6a947b_l3.png)
![Rendered by QuickLaTeX.com \[ p = \frac{N_a - N_d}{2} + \sqrt{\bigg(\frac{N_a - N_d}{2}\bigg)^2 + n_i^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8b5f4dfd11112fed5fac73b86ec06631_l3.png)
- 定义本征载流子浓度(Intrinsic Carrier Concentration)
- 半导体的类型
- 本征半导体(Intrinsic Semiconductor)我们有
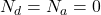 ,故
,故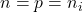
- N型半导体(N-Type Semiconductor)我们有
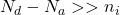 ,故
,故
进一步,如果![Rendered by QuickLaTeX.com \[ n = N_d - N_a,\; p = n_i^2/(N_d - N_a). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dd7b8348de3b19de6136790d9b605686_l3.png)
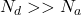 ,那么
,那么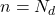 ,
,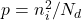
- P型半导体(P-Type Semiconductor)我们有
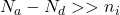 ,故
,故
进一步,如果![Rendered by QuickLaTeX.com \[ p = N_a - N_d,\; n = n_i^2/(N_a - N_d). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bb83cf644f9f1b26b5ad3c96681d3567_l3.png)
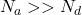 ,那么
,那么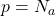 ,
,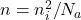
- 本征半导体(Intrinsic Semiconductor)我们有
- 电子和空穴都能形成电流,二者称为载流子(Carrier),载流子分为多数载流子(Majority Carrier)和少数载流子(Minority Carrier)。在N型半导体中,电子是多数载流子,空穴是少数载流子;在P型半导体中,空穴是多数载流子,电子是少数载流子