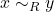至大无外,谓之大一;至小无内,谓之小一。——《庄子·天下》
无限集合
- 由Lebesgue测度可知,算术化将微积分化归为实数,公理化将实数化归为集合。因此,无穷小微分的矛盾之处,实际上是无限集合的矛盾之处
- 有限主义者(Finitist)认为,只存在有限集合。比如,根据计算和信息,可计算的实数是有限的。既然不存在无穷大,那么也不存在无穷小
- 在浮点算术中,比最大(大一)更大会出现上溢(至大无外),比最小(小一)更小会出现下溢(至小无内)
- 如果存在无穷大,那么它的倒数为无穷小。无限集合的性质,是有限集合的性质,经过形式化得到的
- //
- 计数可以分为基数(Cardinal)和序数(Ordinal)
- 基数对应于大小(Size)
- 序数对应于顺序(Order)
- 在生命演化的计算原理中,我们考虑von Neumann的生命哲学;在这里,我们考虑von Neumann序数。二者可以和《庄子·齐物论》进行比较
- 既已为一矣,且得有言乎?
![Rendered by QuickLaTeX.com \[ 0 = \emptyset. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-67bf0bb8946b9cafc0737221628dcca4_l3.png)
- 既已谓之一矣,且得无言乎?
![Rendered by QuickLaTeX.com \[ 1 = \{ \emptyset \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7af439ace817a0947c718c86af785e6c_l3.png)
- 一与言为二。
![Rendered by QuickLaTeX.com \[ 2 = \{ \emptyset, \{ \emptyset \} \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a234b9fc6ccebf862f0083cd0d02159c_l3.png)
- 二与一为三。
![Rendered by QuickLaTeX.com \[ 3 = \{ \emptyset, \{ \emptyset \}, \{ \emptyset,\; \{ \emptyset \} \} \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-befe157c8d48e157372f54595025dfaa_l3.png)
- 自此以往,巧历不能得,而况其凡乎?
![Rendered by QuickLaTeX.com \[ 0, 1, 2, 3, \ldots, \omega. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-366ab41a171518caaaac1e7bd05852cc_l3.png)
- 故自无适有,以至于三,而况自有适有乎?
![Rendered by QuickLaTeX.com \[ \omega, \omega + 1, \ldots, 2\omega, \ldots, \omega^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1d37acb2a40f3cc17fb0ce46d0e694b5_l3.png)
- 无适焉,因是已!
其中,最后一项为Epsilon数,它是不动点方程![Rendered by QuickLaTeX.com \[ \omega^2, \ldots, \omega^\omega, \ldots, \omega^{\omega^{.^{.^{.}}}}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-431d1199eafd45a2725452d4d394abf1_l3.png)
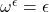 的解
的解
- 既已为一矣,且得有言乎?
- Epsilon数,可以用于证明算术的相容性,它超越于算术系统之外。如果不使用Epsilon数,那么由Gödel不完备定理可知,我们无法证明算术的相容性
映射
- 在数学中,我们使用映射(Map);在计算机科学中,我们使用函数(Function)。数学的函数 –> 返回值为“数”的映射,计算机科学的函数 –> 一般的映射
- 实变函数
- 一元函数 –> 参数为一个实数,返回值为一个实数
- 多元函数 –> 参数为多个实数,返回值为一个实数
- 复变函数
- 单复变函数 –> 参数为一个复数,返回值为一个复数
- 多复变函数 –> 参数为多个复数,返回值为一个复数
- 一般的映射
- (定义域,单)单值映射在定义域上单,多值映射在定义域上非单
- (定义域,满)全映射在定义域上满,偏映射在定义域上非满
- (值域,单)单射在值域上单,非单射在值域上非单
- (值域,满)满射在值域上满,非满射在值域上非满
- 实变函数
- 我们通常说的映射,实际上是指“单值映射 + 全映射”,它在定义域上既单又满。我们通常说的逆映射,实际上是指“单射 + 满射”,它在值域上既单又满。二者是对偶的
- 单值映射 + 全映射 –> 映射
- 单射 + 满射 –> 逆映射
- 映射 + 逆映射 –> 双射
关系
- 映射
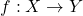 可以用如下关系来描述,
可以用如下关系来描述,
这里,集合![Rendered by QuickLaTeX.com \[ x \sim_R y \text{ if and only if } f(x) = y. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3ba3bdd90f4ad80dcf15f02020dcbb97_l3.png)
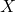 、
、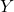 之间的关系为
之间的关系为
如果![Rendered by QuickLaTeX.com \[ R \subset X \times Y. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e5c3dbacfe740df6a8f181f208455fc8_l3.png)
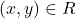 ,那么我们记
,那么我们记