最大化Shannon熵
- Lagrange乘子法和最优化问题
- (信息理论)在信噪比和位深中,Lagrange乘子法 –> 最大化微分熵 –> 信道容量
- (量子统计力学)在半导体的电子和空穴中,Lagrange乘子法 –> 最大化将电子分配到状态中的方法数 –> Fermi分布
- (统计热动力学)在这里,Lagrange乘子法 –> 最大化Shannon熵 –> Gibbs分布
- 由Hamilton方程可知,Hamiltonian为相空间中某一状态的能量
- 为了最大化Shannon熵,我们使用Lagrange乘子法。令
![Rendered by QuickLaTeX.com \[ L = -\sum_i p_i\ln p_i - \alpha\varphi_1 - \beta\varphi_2, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3609cb92107b74267fd9230f158575c7_l3.png)
其中,
![Rendered by QuickLaTeX.com \[ \varphi_1 = \sum_i p_i - 1,\; \varphi_2 = \sum_i \mathcal{H}_ip_i - U. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-44d15cf2f6136e42f5e54badd472ed37_l3.png)
- 对于Gibbs分布,我们可以计算更多的信息理论中的量。首先,
![Rendered by QuickLaTeX.com \[ \ln\mathbb{P}(X_\beta = x_i) = -\beta\mathcal{H}(x_i) - \ln Z, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9f3e90e6c527378c5c1e7aa9e85d1edf_l3.png)
其中,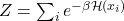 称为配分函数,它不依赖于概率分布
称为配分函数,它不依赖于概率分布
- (Shannon熵)我们有
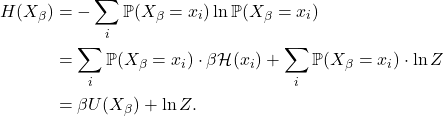
因此,我们可以得到如下的能量-熵关系(Energy-Entropy Relation);由于Shannon熵可以视为信息量,故它也是能量-信息关系(Energy-Information Relation)
![Rendered by QuickLaTeX.com \[ U(X_\beta) - \frac 1\beta H(X_\beta) = -\frac 1\beta\ln Z. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f4b66982b8dd772aa421d57c093be311_l3.png)
- (交叉熵)我们有
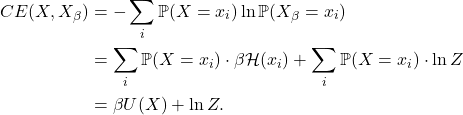
因此,我们可以得到如下的能量-交叉熵关系(Energy-CrossEntropy Relation)
![Rendered by QuickLaTeX.com \[ U(X) - \frac 1\beta CE(X, X_\beta) = -\frac 1\beta\ln Z. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4fb801bc368e822bef0e3571d71ba322_l3.png)
- (KL散度)由能量-交叉熵关系,
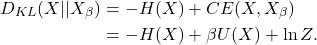
由能量-熵关系,
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} D_{KL}(X || X_\beta) &= -H(X) + \beta U(X) + H(X_\beta) - \beta U(X_\beta) \\ &= \beta\bigg[U(X) - \frac 1\beta H(X)\bigg] - \beta\bigg[U(X_\beta) - \frac 1\beta H(X_\beta)\bigg]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9b7acedaa4b3129a84b00eed1c4ea445_l3.png)
- 如果我们定义自由能为
![Rendered by QuickLaTeX.com \[ F = U - \frac 1\beta H, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e2f92d1b275072599a01c47a371415e8_l3.png)
那么,当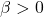 时,
时,
![Rendered by QuickLaTeX.com \[ F(X) - F(X_\beta) = \frac 1\beta D_{KL}(X || X_\beta) \geq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6d08a7e0287609950baa55c6df69159e_l3.png)
Gibbs分布既可以最大化Shannon熵,也可以最小化自由能。此时,我们称系统位于热动力学平衡态(Thermodynamic Equilibrium)
- 在内能不变的约束下,Gibbs分布可以最大化Shannon熵
- 在无约束下,Gibbs分布可以最小化自由能
- 我们通常用自由能是否最小,来判断系统是否位于热动力学平衡态,并且KL散度可以用于衡量系统状态、热动力学平衡态之间的接近程度
- 最后,Gibbs分布的内能、Shannon熵、自由能可以由配分函数得到
电路中的噪声
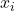 的概率为
的概率为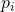 ,那么
,那么![Rendered by QuickLaTeX.com \[ \sum_i p_i = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-05a8acd2cee1acbecdccd28208cc996e_l3.png)
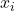 的Hamiltonian为
的Hamiltonian为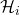 ,那么内能为Hamiltonian的数学期望
,那么内能为Hamiltonian的数学期望![Rendered by QuickLaTeX.com \[ \sum_i \mathcal{H}_ip_i = U. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-82c7dbcdb63733b643a29273eb0ac216_l3.png)
![Rendered by QuickLaTeX.com \[ L = -\sum_i p_i\ln p_i - \alpha\varphi_1 - \beta\varphi_2, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3609cb92107b74267fd9230f158575c7_l3.png)
![Rendered by QuickLaTeX.com \[ \varphi_1 = \sum_i p_i - 1,\; \varphi_2 = \sum_i \mathcal{H}_ip_i - U. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-44d15cf2f6136e42f5e54badd472ed37_l3.png)
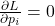 ,可得
,可得![Rendered by QuickLaTeX.com \[ p_i = e^{-1 - \alpha - \beta\mathcal{H}_i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5952257ae5e32563e70f2b293772dfda_l3.png)
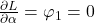 ,可得Gibbs分布
,可得Gibbs分布![Rendered by QuickLaTeX.com \[ \mathbb{P}(X_\beta = x_i) = \frac{e^{-\beta\mathcal{H}(x_i)}}{\sum_i e^{-\beta\mathcal{H}(x_i)}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dcaa73483d94f5732e65342c9205b7a6_l3.png)
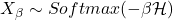
![Rendered by QuickLaTeX.com \[ \ln\mathbb{P}(X_\beta = x_i) = -\beta\mathcal{H}(x_i) - \ln Z, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9f3e90e6c527378c5c1e7aa9e85d1edf_l3.png)
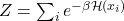 称为配分函数,它不依赖于概率分布
称为配分函数,它不依赖于概率分布
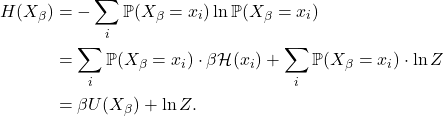
![Rendered by QuickLaTeX.com \[ U(X_\beta) - \frac 1\beta H(X_\beta) = -\frac 1\beta\ln Z. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f4b66982b8dd772aa421d57c093be311_l3.png)
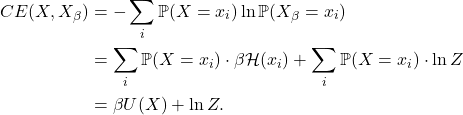
![Rendered by QuickLaTeX.com \[ U(X) - \frac 1\beta CE(X, X_\beta) = -\frac 1\beta\ln Z. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4fb801bc368e822bef0e3571d71ba322_l3.png)
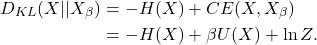
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} D_{KL}(X || X_\beta) &= -H(X) + \beta U(X) + H(X_\beta) - \beta U(X_\beta) \\ &= \beta\bigg[U(X) - \frac 1\beta H(X)\bigg] - \beta\bigg[U(X_\beta) - \frac 1\beta H(X_\beta)\bigg]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9b7acedaa4b3129a84b00eed1c4ea445_l3.png)
![Rendered by QuickLaTeX.com \[ F = U - \frac 1\beta H, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e2f92d1b275072599a01c47a371415e8_l3.png)
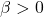 时,
时,![Rendered by QuickLaTeX.com \[ F(X) - F(X_\beta) = \frac 1\beta D_{KL}(X || X_\beta) \geq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6d08a7e0287609950baa55c6df69159e_l3.png)