拓扑空间、链复形、同调群
- 由奇异同调群的定义可知,对于拓扑空间的奇异同调群,其建立过程为
然而,![Rendered by QuickLaTeX.com \[ X \mapsto C_*(X) \mapsto H_*(X) \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-415cfc4e639741ce17a5071b8977f22f_l3.png)
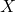 的定义域为全体拓扑空间,
的定义域为全体拓扑空间,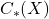 的定义域为全体链复形,
的定义域为全体链复形,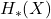 的定义域为全体Abel群。类似于Lebesgue测度中的Russell的类型论,全体集合(高阶类型)不再是一个集合(低阶类型);同样地,全体拓扑空间、链复形、Abel群也不再是一个集合
的定义域为全体Abel群。类似于Lebesgue测度中的Russell的类型论,全体集合(高阶类型)不再是一个集合(低阶类型);同样地,全体拓扑空间、链复形、Abel群也不再是一个集合 - 因此,上面的建立过程不是集合之间的映射,而是范畴之间的函子
- 拓扑空间、链复形、Abel群,它们称为对象
- 连续映射、链映射、Abel群的同态,它们称为态射
- 函子既作用于对象,也作用于态射。比如,拓扑空间的奇异链复形函子为
链复形的同调函子为![Rendered by QuickLaTeX.com \[ Top \to Comp,\; X \mapsto C_*(X),\; f \mapsto f_*. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1fa385be43cf0d48bdd3e41e88cbe8b8_l3.png)
这里,![Rendered by QuickLaTeX.com \[ Comp \to Ab,\; C_* \mapsto H_*,\; f \mapsto f_*. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-793b587cfc58fee3d3862b25a9125eec_l3.png)
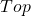 为拓扑空间范畴、
为拓扑空间范畴、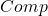 为链复形范畴、
为链复形范畴、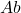 为Abel群范畴
为Abel群范畴
一般的链复形
- 链复形范畴、上链复形范畴互为反范畴,链复形的指标不断下降,上链复形的指标不断上升。下面,我们只考虑链复形范畴
- 一般的链复形
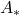 为Abel群、Abel群的同态形成的序列
为Abel群、Abel群的同态形成的序列
满足![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ \cdots \ar[r] & A_n \ar[r]^-{\partial_n} & A_{n - 1} \ar[r] & \cdots } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a2dbf179a766e67979b6974e9da99567_l3.png)
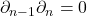
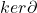 中的元素称为闭链,
中的元素称为闭链,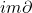 中的元素称为边缘链。因为链复形满足
中的元素称为边缘链。因为链复形满足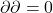 ,所以
,所以![Rendered by QuickLaTeX.com \[ im\partial_{n + 1} \subset ker\partial_n \subset A_n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8c352232870ecf5f04cdff7b829a67ff_l3.png)
- 链复形
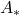 的同调群为
的同调群为![Rendered by QuickLaTeX.com \[ H_n = ker\partial_n / im\partial_{n + 1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fcd253380e70a261ea5a268a7aca4e85_l3.png)
- 一般的链映射
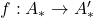 为
为
满足![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ \cdots \ar[r] & A_n \ar[r]^-{\partial_n} \ar[d]^-{f_n} & A_{n - 1} \ar[r] \ar[d]^-{f_{n - 1}} & \cdots \\ \cdots \ar[r] & A_n' \ar[r]^-{\partial_n'} & A_{n - 1}' \ar[r] & \cdots } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-53773b472c5a0cd8ee110d21ee761639_l3.png)
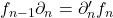
- 链映射将闭链映射到闭链,将边缘链映射到边缘链,
![Rendered by QuickLaTeX.com \[ \partial_na_n = 0 \Rightarrow \partial_n'f_na_n = f_{n - 1}\partial_na_n = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-80bebd6ff691ae07572899e221f29de0_l3.png)
![Rendered by QuickLaTeX.com \[ a_{n - 1} = \partial_na_n \Rightarrow f_{n - 1}a_{n - 1} = f_{n - 1}\partial_na_n = \partial_n'f_na_n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c170473995737a4dd6528405bfdd6978_l3.png)
- 链映射
 诱导的同态为
诱导的同态为
这里,代表元素![Rendered by QuickLaTeX.com \[ f_*: H_n \to H_n',\; [a_n] \mapsto [f_na_n]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6a8e5d4e92ae3789d0a50642ad604c6a_l3.png)
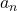 为闭链,并且边缘链
为闭链,并且边缘链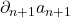 等价于0
等价于0
- 链映射将闭链映射到闭链,将边缘链映射到边缘链,
- 链复形的同调函子为
![Rendered by QuickLaTeX.com \[ Comp \to Ab,\; A_* \to H_*,\; f \mapsto f_*. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bfbb3b8ab791cbe12fc6e580b7b52701_l3.png)
- 我们希望同调群为拓扑不变量,即同胚的拓扑空间,具有同构的链复形、同调群
- 为了定义同构,我们需要复合、恒等
为了得到不变量,我们需要函子保持复合、恒等![Rendered by QuickLaTeX.com \[ g \circ f = id,\; f \circ g = id. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-121bd0048910791f5516f8e846ac86a8_l3.png)
![Rendered by QuickLaTeX.com \[ F(g \circ f) = F(g) \circ F(f),\; F(id) = id. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fda39c7a3d6103d459463fc0f36bd997_l3.png)
- 由此可知,函子保持同构
故同胚的拓扑空间,具有同构的链复形、同调群![Rendered by QuickLaTeX.com \[ F(g) \circ F(f) = id,\; F(f) \circ F(g) = id. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-05700b838a55ba7b3de27bebf11b9872_l3.png)
链复形的短正合列、同调群的长正合列
- 正合列是直和分解的推广,它通常用于将大的空间分解为小的空间。比如
其中,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ 0 \ar[r] & A \ar[r]^-{i} & A \oplus B \ar[r]^-{p} & B \ar[r] & 0 } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9f00dab58e7453e1862709913d5ab9b9_l3.png)
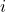 为含入
为含入![Rendered by QuickLaTeX.com \[ i: A \to A \oplus B,\; a \mapsto (a, 0), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-28186f9c8093a85e77c268fe197d292f_l3.png)
 为投影
为投影
因此,![Rendered by QuickLaTeX.com \[ p: A \oplus B \to B,\; (a, b) \mapsto b. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e3656fa31e9d90b85d84ec9cbfd29281_l3.png)
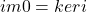 ,
,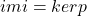 ,
,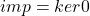 。我们称上面的序列在中间三个Abel群上是正合的,它构成一个短正合列
。我们称上面的序列在中间三个Abel群上是正合的,它构成一个短正合列 - 拓扑空间分解为子空间,通常可以得到奇异链复形的短正合列。我们需要由链复形的短正合列,计算同调群之间的关系
- 链复形的短正合列为
由正合的定义,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ 0 \ar[r] & A_* \ar[r]^-{i} & A_*' \ar[r]^-{p} & A_*'' \ar[r] & 0 } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-24e203c2c0147675f67e14d61fa3322a_l3.png)
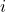 为单射、
为单射、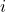 的像为
的像为 的核、
的核、 为满射。它可以展开为
为满射。它可以展开为
下面,记一般的链为![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ 0 \ar[r] & A_{n + 1} \ar[r]^-{i_{n + 1}} \ar[d]^-{\partial_{n + 1}} & A_{n + 1}' \ar[r]^-{p_{n + 1}} \ar[d]^-{\partial_{n + 1}'} & A_{n + 1}'' \ar[r] \ar[d]^-{\partial_{n + 1}''} & 0 \\ 0 \ar[r] & A_n \ar[r]^-{i_n} \ar[d]^-{\partial_n} & A_n' \ar[r]^-{p_n} \ar[d]^-{\partial_n'} & A_n'' \ar[r] \ar[d]^-{\partial_n''} & 0 \\ 0 \ar[r] & A_{n - 1} \ar[r]^-{i_{n - 1}} & A_{n - 1}' \ar[r]^-{p_{n - 1}} & A_{n - 1}'' \ar[r] & 0 } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-599b294805492d60aaa8b557a48605a9_l3.png)
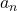 、闭链为
、闭链为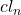 、边缘链为
、边缘链为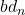
- 链复形的短正合列为
- 由于链映射诱导同调群的同态,故
我们需要考察![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ H_n \ar[r]^-{i_*} & H_n' \ar[r]^-{p_*} & H_n'' } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1b62aefe09279e39dffcb330800ffd18_l3.png)
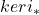 、
、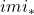 、
、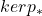 、
、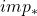
- (在
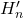 上正合)由
上正合)由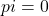 ,可得
,可得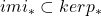 。反过来,由
。反过来,由![Rendered by QuickLaTeX.com [cl_n'] \in kerp_*](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8a2c0fac2c97e561cbaf069f884592ff_l3.png) 可以得到
可以得到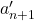 ,
,
然后,由![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ a_{n + 1}' \ar[r] & a_{n + 1}'' \ar[d] \\ cl_n' \ar[r] & bd_n'' } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9f73d3ca12a847900b30ecf6dc94fdaa_l3.png)
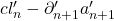 可以得到
可以得到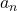 ,
,
由下方的0可知,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ a_n \ar[r] & cl_n' - \partial_{n + 1}'a_{n + 1}' \ar[r] \ar[d] & 0 \\ 0 \ar[r] & 0 & {} } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7cca982b27a554d0137ef27001a886e3_l3.png)
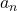 为闭链,故
为闭链,故![Rendered by QuickLaTeX.com [cl_n' - \partial_{n + 1}'a_{n + 1}'] \in imi_*](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a1ef80c00d5cd1644ee1d38d6e0dac96_l3.png)
- (
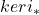 )由
)由![Rendered by QuickLaTeX.com [cl_n] \in keri_*](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9d709cca4e2985f8b0de31ce0130262a_l3.png) 可以得到
可以得到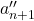 ,
,
由下方的0可知,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ {} & a_{n + 1}' \ar[r] \ar[d] & a_{n + 1}'' \\ cl_n \ar[r] & bd_n' \ar[r] & 0 } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ff2162930c472702080ebd5c9d76b055_l3.png)
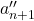 为闭链。反过来,由
为闭链。反过来,由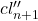 可以得到
可以得到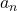 ,
,
由下方的0可知,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ {} & a_{n + 1}' \ar[r] \ar[d] & cl_{n + 1}'' \ar[d] \\ a_n \ar[r] & bd_n' \ar[r] \ar[d] & 0 \\ 0 \ar[r] & 0 & {} } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3739d9c95ec879064ce7ff6afc470e75_l3.png)
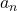 为闭链。因此,我们实际上定义了
为闭链。因此,我们实际上定义了
满足![Rendered by QuickLaTeX.com \[ \partial: H_{n + 1}'' \to H_n,\; [cl_{n + 1}''] \mapsto [cl_n], \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e365df12f993167c524995f53d286c64_l3.png)
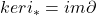
- (
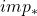 )上面已经得到了同调群的正合三角
)上面已经得到了同调群的正合三角
我们还剩下![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ {} & H_*' \ar[dr]^-{p_*} & {} \\ H_* \ar[ur]^-{i_*} & {} & H_*'' \ar[ll]^-{\partial} } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8abb02d695c15754e37cec1080ce0938_l3.png)
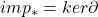 需要证明。由
需要证明。由![Rendered by QuickLaTeX.com [cl_{n + 1}''] \in imp_*](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-54a10a337f90e8260f009615f3b5288e_l3.png) 可以得到
可以得到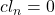 ,从而
,从而![Rendered by QuickLaTeX.com [cl_{n +1}''] \in ker\partial](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d313ae4ca0257911dee3cad87b65fe55_l3.png) ,
,
反过来,由![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ {} & cl_{n + 1}' \ar[r] \ar[d] & cl_{n + 1}'' \\ 0 \ar[r] & 0 & {} } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-41abd0c903363f673b594900357fc7bd_l3.png)
![Rendered by QuickLaTeX.com [cl_{n + 1}''] \in ker\partial](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-64cce2ea2593426498b4315983cc7d1e_l3.png) 可以得到
可以得到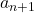 ,
,
故![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ a_{n + 1} \ar[d] & a_{n + 1}' \ar[r] \ar[d] & cl_{n + 1}'' \\ bd_n \ar[r] & bd_n' & {} } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-27e33c96accd2c40f1b547665ad64a62_l3.png)
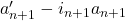 为闭链,并且
为闭链,并且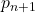 将其映射到
将其映射到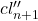 ,从而
,从而![Rendered by QuickLaTeX.com [cl_{n +1}''] \in imp_*](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc6fb7c783ce8296053e610f37d80628_l3.png)
- (在
- 最终,我们将同调群的正合三角展开为同调群的长正合列,
在上面的证明中,我们反复使用了有向图的箭头追踪。因此,范畴论的关键在于有向图的结构![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ \cdots \ar[r] & H_{n + 1}' \ar[r]^-{p_*} & H_{n + 1}'' \ar[r]^-{\partial} & H_n \ar[r]^-{i_*} & H_n' \ar[r]^-{p_*} & H_n'' \ar[r] & \cdots } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e49898fbaa9d38388fe1d5c17d37347d_l3.png)