微分
- 数列的分析
- 差分
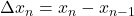
- 求和
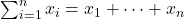
- 差分、求和是逆运算
![Rendered by QuickLaTeX.com \[ \sum_{i = 1}^n\bigg(\Delta x_i\bigg) = x_n - x_0,\; \Delta\bigg(\sum_{i = 1}^n x_i\bigg) = x_n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-74dd5ba5fd614070b9daa1d2ce9c1a4f_l3.png)
- 差分
 上的分析
上的分析
- 差分
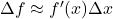 。差分的极限不是微分
。差分的极限不是微分![Rendered by QuickLaTeX.com \[ \Delta f \not\to df = f'(x)dx. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-24e366733c508252da3b49f45653ef7c_l3.png)
- 然而,差商的极限是微商,求和的极限是积分
- 差商
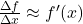 。取极限可得导数
。取极限可得导数![Rendered by QuickLaTeX.com \[ \frac{\Delta f}{\Delta x} \to \frac{df}{dx} = f'(x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ff5b5785f911476f11cc301c0db7e271_l3.png)
- 求和
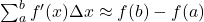 。取极限可得Newton-Leibniz公式
。取极限可得Newton-Leibniz公式![Rendered by QuickLaTeX.com \[ \sum_a^b f'(x)\Delta x \to \int_a^b f'(x)dx = f(b) - f(a). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-39d0cdb5c2f63065e62c7853c1468a00_l3.png)
- 差商
- 我们可以形式化地定义微分
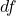 。微积分(Calculus)的精髓就在于有限差分的几何直观,以及无穷小微分的形式化演算
。微积分(Calculus)的精髓就在于有限差分的几何直观,以及无穷小微分的形式化演算 - 形式化演算的好处在于不依赖于人的直觉,所以可以用计算机来计算。比如通过证明论的公理化演算(Axiomatic Calculus)、类型论的Lambda演算(Lambda Calculus),计算机可以自动证明定理
- 差分
切空间
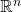 上的分析
上的分析
- 在一点
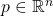 处,
处,![Rendered by QuickLaTeX.com \[ df = \sum_i \partial_if \cdot dx^i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-41b8ab7e31305523f8a9a7cbda66354d_l3.png)
- 由数值线性代数可知,如果
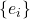 为线性空间
为线性空间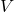 的基底,
的基底,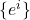 为对偶线性空间
为对偶线性空间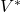 的对偶基底,那么
的对偶基底,那么
类似地,如果![Rendered by QuickLaTeX.com \[ f = \sum_i \langle{f, e_i}\rangle \cdot e^i,\; f \in V^*. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-93dd58e64faa133b8fc75bcac8af1ce0_l3.png)
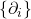 为线性空间
为线性空间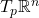 的基底,
的基底,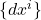 为对偶线性空间
为对偶线性空间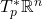 的对偶基底,那么对于
的对偶基底,那么对于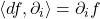 ,我们有相同的公式
,我们有相同的公式
当指标![Rendered by QuickLaTeX.com \[ df = \sum_i \langle{df, \partial_i}\rangle \cdot dx^i,\; df \in T_p^*\mathbb{R}^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b9d52a3fac04dcae3c0ee35d84362d61_l3.png)
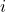 同时出现在上方、下方时,我们可以省略求和符号
同时出现在上方、下方时,我们可以省略求和符号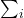 ,这称为Einstein求和约定
,这称为Einstein求和约定
- 在一点
- 接下来我们考虑一般的
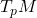 。在计算机图形学中,
。在计算机图形学中, 中的曲面
中的曲面 可以用参数表示来描述,
可以用参数表示来描述,![Rendered by QuickLaTeX.com \[ (u^1, u^2) \mapsto (x^1, x^2, x^3). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e22c7374af33aa870d311eecda4c7ac9_l3.png)
- 设
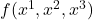 为函数。
为函数。 沿着向量
沿着向量 的方向导数为
的方向导数为![Rendered by QuickLaTeX.com \[ \frac{\partial f}{\partial v} = \frac{\partial f}{\partial x^i} \cdot v^i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-21faa22bf773f7b0bbc702a3f3b2762c_l3.png)
 沿着参数
沿着参数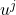 的偏导数为
的偏导数为![Rendered by QuickLaTeX.com \[ \frac{\partial f}{\partial u^j} = \frac{\partial f}{\partial x^i} \cdot \frac{\partial x^i}{\partial u^j}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-addb2446a6775fe4bea6e6e955e98b57_l3.png)
- 我们有如下的、微分算子和向量之间的对应
其中,![Rendered by QuickLaTeX.com \[ \frac{\partial}{\partial u^j} \mapsto \bigg(\frac{\partial x^1}{\partial u^j}, \frac{\partial x^2}{\partial u^j}, \frac{\partial x^3}{\partial u^j}\bigg) = v, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-57f1ecff4b926b285df33450d10fc665_l3.png)
 为
为 在
在 中的切向量,并且所有
中的切向量,并且所有 张成
张成 在
在 中的切平面。因此,
中的切平面。因此,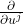 对应于切向量,
对应于切向量,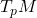 对应于切空间
对应于切空间
- 设
- 对于
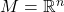 ,我们有
,我们有
故![Rendered by QuickLaTeX.com \[ \frac{\partial}{\partial x^j} \mapsto (0, \ldots, 1 (j^{\text{th}}), \ldots, 0). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e1368ace1d38de435673ad744496e5f_l3.png)
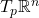 为
为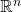 本身。从而,微分
本身。从而,微分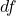 对应于余切向量,
对应于余切向量,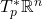 对应于余切空间
对应于余切空间
从切空间到局部
- 设
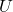 、
、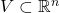 为开集,
为开集,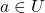
- 如果
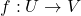 为
为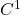 映射,那么
映射,那么 在
在 处的微分为切空间上的切映射,
处的微分为切空间上的切映射,
这恰好是![Rendered by QuickLaTeX.com \[ df_a: T_aU = \mathbb{R}^n \to T_{f(a)}V = \mathbb{R}^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4bd25876fc11eda90dda611cd18ec303_l3.png)
 在
在 处的Jacobi矩阵,我们将其记为
处的Jacobi矩阵,我们将其记为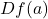 。下面的逆映射定理指出,一点处的切映射可以确定该点处局部的拓扑性质
。下面的逆映射定理指出,一点处的切映射可以确定该点处局部的拓扑性质 - (逆映射定理)如果
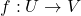 为
为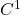 映射,并且
映射,并且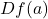 可逆,那么
可逆,那么 在
在 处局部为
处局部为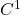 微分同胚
微分同胚
- 我们需要寻找
 的开邻域
的开邻域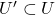 ,使得
,使得
为![Rendered by QuickLaTeX.com \[ f|_{U'}: U' \to f(U') \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-23eafabf9a39fb9c6d2fd835a638715a_l3.png)
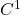 微分同胚。关键在于证明
微分同胚。关键在于证明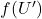 为开集,我们需要对任意固定的
为开集,我们需要对任意固定的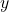 ,求解非线性方程
,求解非线性方程
在数值计算中,我们使用迭代方法求解非线性方程,比如不动点定理。在从不动点定理到编程语言中,我们需要弱完备空间的连续映射,或者强完备空间的递增映射;在完备度量空间中,我们需要完备度量空间的压缩映射![Rendered by QuickLaTeX.com \[ y = f(x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-20282ec1fc97a6fcf8e7739fd1f958c9_l3.png)
- 将上述方程转化为不动点方程
然后取![Rendered by QuickLaTeX.com \[ x = \phi_y(x) = x + Df(a)^{-1}[y - f(x)], \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-27d9ab263e1da4e84757a929c33e53ef_l3.png)
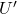 为
为 的凸的开邻域,满足
的凸的开邻域,满足
对线段![Rendered by QuickLaTeX.com \[ ||D\phi_y(x)|| = ||I - Df(a)^{-1}Df(x)|| \leq \frac 12,\; x \in U'. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-61b74c340adfa28ee2fece8d421c8a56_l3.png)
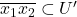 使用微分不等式,可得
使用微分不等式,可得
下面我们证明![Rendered by QuickLaTeX.com \[ ||\phi_y(x_1) - \phi_y(x_2)|| \leq \frac 12||x_1 - x_2||. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e081f6da28bffadeed462e107f35a8e5_l3.png)
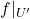 为
为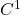 微分同胚
微分同胚 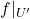 为双射
为双射
- 只需证明
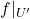 为单射,如果
为单射,如果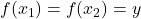 ,
,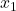 、
、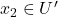 ,那么
,那么
因此,![Rendered by QuickLaTeX.com \[ ||x_1 - x_2|| = ||\phi_y(x_1) - \phi_y(x_2)|| \leq \frac 12||x_1 - x_2||. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ba8d801a34b27d16957eb8df17459d4d_l3.png)
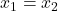
- 只需证明
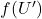 为开集
为开集
- 设
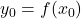 任意固定,其中
任意固定,其中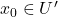 。那么,
。那么,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} ||\phi_y(x_0) - x_0|| &= ||x_0 + Df(a)^{-1}[y - f(x_0)] - x_0|| \\ &\leq ||Df(a)^{-1}|| \cdot ||y - y_0||. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-49064e4f8b6177986b537cff7397e7f5_l3.png)
- 取
 、
、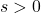 满足
满足
那么,对任意![Rendered by QuickLaTeX.com \[ \overline{B_r(x_0)} \subset U',\; s \leq ||Df(a)^{-1}||^{-1} \cdot \frac 12r. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4e43fba6746cfc23b2d1ef9453c09a02_l3.png)
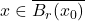 、
、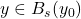 ,我们有
,我们有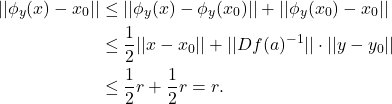
- 由此可知,对任意
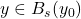 ,
,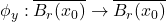 为完备度量空间的压缩映射。由不动点定理,存在
为完备度量空间的压缩映射。由不动点定理,存在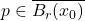 使得
使得
即![Rendered by QuickLaTeX.com \[ p = \phi_y(p) = p + Df(a)^{-1}[y - f(p)]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-20d9d7f195894d82a66e7cef49101283_l3.png)
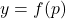 。因此,
。因此,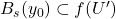 ,
,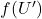 为开集
为开集
- 设
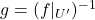 为
为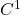 映射
映射
- 我们使用差分
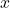 、
、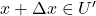 ,以及
,以及
由![Rendered by QuickLaTeX.com \[ f(x) = y,\; f(x + \Delta x) = y + \Delta y. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-398bd33fa4d4b81b11fa8270841df8d8_l3.png)
可得![Rendered by QuickLaTeX.com \[ ||\Delta x - Df(a)^{-1}\Delta y|| = ||\phi_y(x + \Delta x) - \phi_y(x)|| \leq \frac 12||\Delta x||, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3da7d456a02f39fd5dd85e7fb9eb00ec_l3.png)
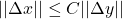 ,即
,即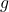 为
为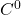 映射
映射 - 由
 为可微映射,当
为可微映射,当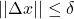 时,我们有
时,我们有
其中,![Rendered by QuickLaTeX.com \[ ||f(x + \Delta x) - f(x) - Df(x)\Delta x|| \leq \epsilon \cdot A \cdot ||\Delta x||, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ad8d9c5b30ed9292a61cab564e9f1d96_l3.png)
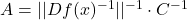 。下面,我们需要进一步取
。下面,我们需要进一步取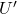 ,使得
,使得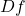 在整个
在整个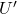 上可逆。当
上可逆。当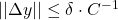 时,我们有
时,我们有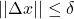 ,并且
,并且
即![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} &\mathrel{\phantom{=}} ||g(y + \Delta y) - g(y) - Df(x)^{-1}\Delta y|| \\ &= ||\Delta x - Df(x)^{-1}[f(x + \Delta x) - f(x)]|| \\ &\leq ||Df(x)^{-1}|| \cdot ||f(x + \Delta x) - f(x) - Df(x)\Delta x|| \\ &\leq ||Df(x)^{-1}|| \cdot \epsilon \cdot A \cdot ||\Delta x|| \\ &\leq \epsilon \cdot ||\Delta y||. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-884e05dfc5a59dfe100d87f352551557_l3.png)
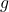 为可微映射,并且
为可微映射,并且![Rendered by QuickLaTeX.com \[ Dg(y) = Df(x)^{-1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ae8ab170c3a8d1600b019632c567b397_l3.png)
- 由
 为
为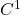 映射,可得
映射,可得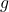 为
为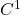 映射,这可以由
映射,这可以由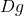 的表达式得到,
的表达式得到,![Rendered by QuickLaTeX.com \[ Dg: y \mapsto x \mapsto Df(x) \mapsto Df(x)^{-1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b038d4504e71d85e0be0747105a66194_l3.png)
- 我们使用差分
- 我们需要寻找
- 逆映射定理对于
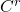 ,
,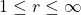 也成立。如果
也成立。如果 为
为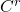 映射,那么
映射,那么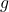 也是
也是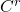 映射,这可以由
映射,这可以由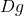 的表达式、数学归纳法得到
的表达式、数学归纳法得到