由学习分享可知,如果你亲手制作了一个音乐,那么你会对其终生难忘
Don’t just be a consumer. Be a producer.——佚名
音的循环
音的概述
- 十二平均律将频率
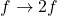 等比例地分为12份,
等比例地分为12份,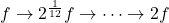
- 它们对应于12阶循环群
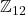
- 它们对应于12阶循环群
- 音名
- 基本音级:C、D、E、F、G、A、B
- 升号♯、降号♭、重升号♯♯、重降号♭♭、还原号♮
- 同音异名:C、C♯/D♭、D、D♯/E♭、E、F、F♯/G♭、G、G♯/A♭、A、A♯/B♭、B
- 音程 :大(Major)、小(Minor)、纯(Perfect)、增(Argumented)、减(Diminished)
- 纯一度(P1):C-C,增一度(A1):C-C♯
- 减二度(d2):C-D♭♭,小二度(m2):C-D♭,大二度(M2):C-D,增二度(A2):C-D♯
- 减三度(d3):C-D-E♭♭,小三度(m3):C-D-E♭,大三度(M3):C-D-E,增三度(A3):C-D-E♯
- 减四度(d4):C-D-E-F♭,纯四度(P4):C-D-E-F,增四度(A4):C-D-E-F♯
- 减五度(d5):C-D-E-F-G♭,纯五度(P5):C-D-E-F-G,增五度(A5):C-D-E-F-G♯
- 减六度(d6):C-D-E-F-G-A♭♭,小六度(m6):C-D-E-F-G-A♭,大六度(M6):C-D-E-F-G-A,增六度(A6):C-D-E-F-G-A♯
- 减七度(d7):C-D-E-F-G-A-B♭♭,小七度(m7):C-D-E-F-B-A-B♭,大七度(M7):C-D-E-F-G-A-B,增七度(A7):C-D-E-F-G-A-B♯
- 减八度(d8):C-D-E-F-G-A-B-C1♭,纯八度(P8):C-D-E-F-G-A-B-C1
- 全音阶(+大二度)
- 生成元为
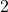 ,对应于子群
,对应于子群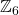
- C-D-E-F♯-G♯-A♯-C1
- C♯-D♯-F-G-A-B-C1♯
- 生成元为
- 减七和弦(+小三度)
- 生成元为
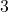 ,对应于子群
,对应于子群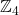
- C-E♭-G♭-A-C1
- C♯-E-G-A♯-C1♯
- D-F-G♯-B-D1
- 生成元为
- 增三和弦(+大三度)
- 生成元为
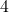 ,对应于子群
,对应于子群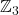
- C-E-G♯-C1
- C♯-F-A-C1♯
- D-F♯-A♯-D1
- D♯-G-B-D1♯
- 生成元为
- 五度圈(+纯四度)
- 生成元为
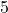 ,对应于子群
,对应于子群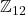
- C-F-A♯-D1♯-G1♯-C2♯-F2♯-B2-E3-A3-D4-G4-C5
- 生成元为
- 三全音(+增四度)
- 生成元为
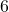 ,对应于子群
,对应于子群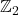
- C-F♯-C1
- C♯-G-C1♯
- D-G♯-D1
- D♯-A-D1♯
- E-A♯-E1
- F-B-F1
- 生成元为
三和弦
- 和声学(Harmonics)研究和弦(Chord),调和分析(Harmonic Analysis)源于音乐中的和声学
- 和声 –> 弦振动 –> 频率 –> Fourier级数、Fourier变换
- 调和 –> 调和函数(Harmonic Functions)
- 和谐 –> 球谐函数(Spherical Harmonics)、谐波(Harmonic Waves)、谐振子(Harmonic Oscillators)
- 大三和弦(Major Triad):C-(+M3)-E-(+m3)-G(=P5),G-(+M3)-B-(+m3)-D1(=P5)
- 小三和弦(Minor Triad):E-(+m3)-G-(+M3)-B(=P5)
- 如果将三和弦的3个音作为3个顶点,那么我们可以得到一个三角形
- 如果考虑所有三和弦的三角形,那么我们可以得到2维平面
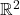 的三角剖分
的三角剖分 - 进一步,如果商掉音的循环(2维周期函数,对应于
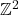 ),那么我们可以得到2维环面
),那么我们可以得到2维环面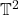 的三角剖分
的三角剖分 - 在计算机图形学中,我们有网格(Mesh)、密铺(Tessellation,通常叫做细分Subdivision);在晶体学中,我们有单位晶胞(Unit Cell)、晶格(Lattice);在拓扑学中,我们有流形的三角剖分(Triangulation)
- 如果考虑所有三和弦的三角形,那么我们可以得到2维平面
这种网格图最早是由数学家莱昂哈德·欧拉(Leonhard Euler)在1739年提出的,其正式名称“Tonnetz”就来自德语(英语直译为“Tone-Network”),字面意思是音的网络。后来的音乐学家胡戈·里曼(Hugo Riemann)等对它又做了深入研究,它将是本书最重要的工具。——《图解和声》
这是数学中的拓扑(Topology)问题,这里不再展开。实际使用时还是平面图更加方便,但要留意循环产生的重复结构。也就是说,网格图虽然可在二维平面上无限延伸,但结构具有周期性,由一些最小的单元胞(Unit cell)像瓷砖一样密铺开来,类似晶体结构中的晶胞或晶格(Lattice)。——《图解和声》
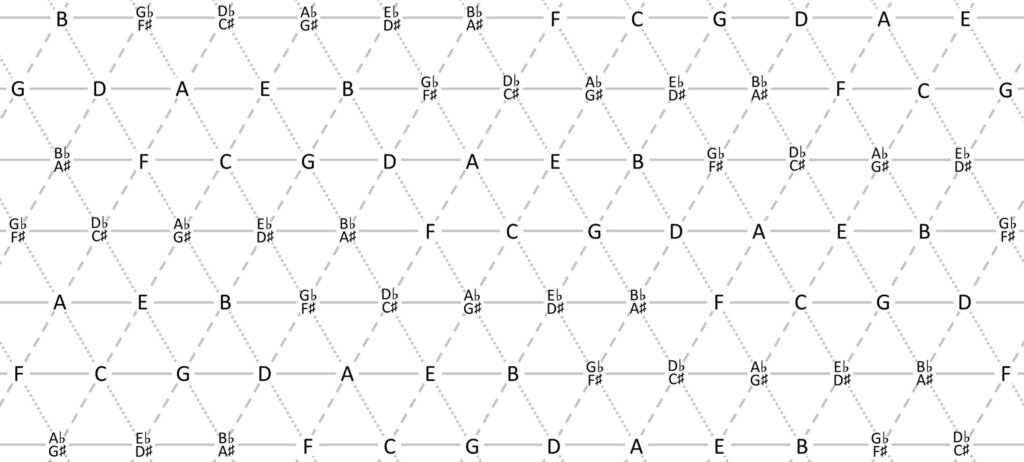
平面的三角剖分
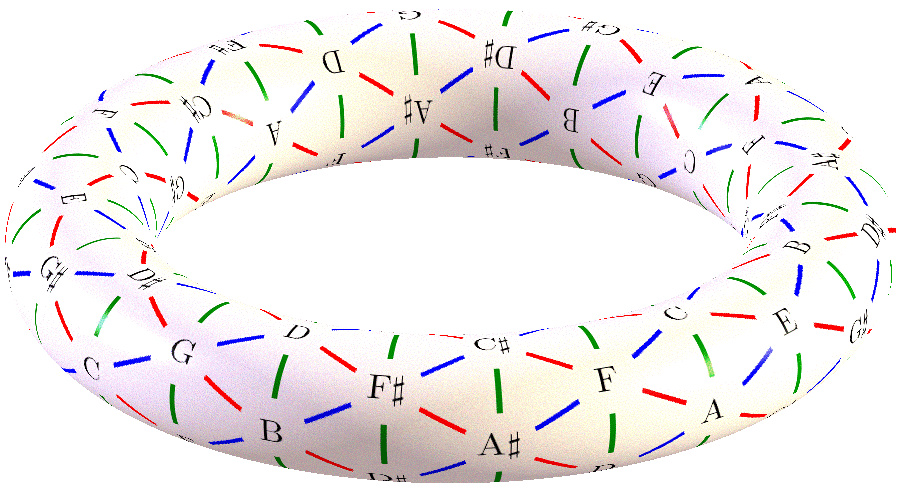
环面的三角剖分
大调和声
五线谱

测试
